PFCステージの伝達関数を素早く導き出す方
力率補正(PFC)ステージのループ補償は、一般に大きな懸案事項とは考えられていません。
確かにPFC回路は、低周波信号のライン電流を整形する必要がありますが、これはPFC回路が本質的にきわめて低速なシステムであるためです。
この理由から、PFCループの補償は、一般に電源を設計する際の重要なステップとは見なされておらず、「帯域幅を大まかに縮小するだけ」のものです。
ただし、ダウンストリーム・コンバータの動作を最適化し、満足な力率を達成するには、他の制御システムと同様にPFCステージを補償して、この不可避なステップを適切に実行する必要があります。
そのため、伝達関数を導き出す必要があります。
PFCステージは低速システム
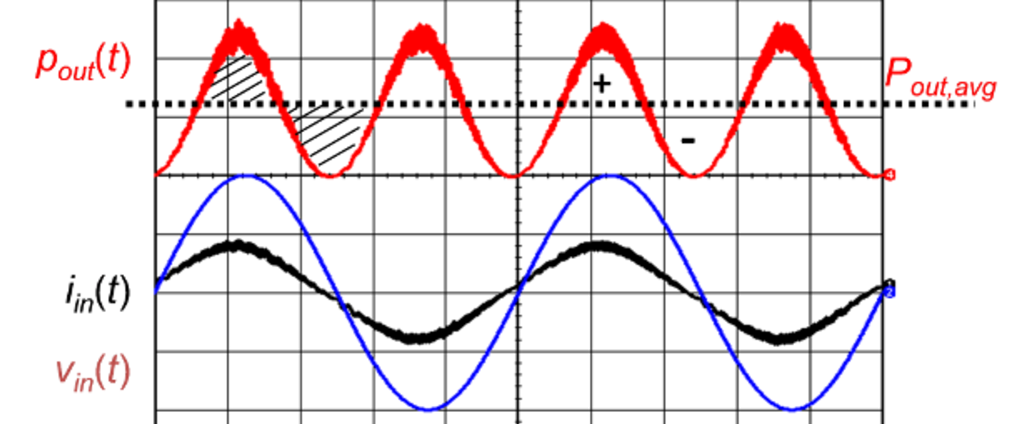
図1を参照してください。
PFC関数の結果、ライン電流(黒線)とライン電圧(青線)は両方とも正弦波です。
したがって、負荷に供給される電力は、赤線で示すように2乗正弦波の形状になっています。
ここで、黒破線が示すように、出力電力はほぼ一定であり、供給される電力は平均値のみ負荷需要に一致しています。
そのため、PFCステージが必要以上の電力を供給している期間が存在します。
「+」記号の領域に注目してください。
このフェーズの間に、出力コンデンサが余剰エネルギーを吸収するため、充電により電荷が増加します。
一方、その後には、PFCステージが供給する電力が必要量を下回る2番目のシーケンスが続きます。
「-」記号の領域に注目してください。
この2番目のケースでは、出力コンデンサが負荷で放電し、エネルギーの不足分を補償します。
その結果、出力電圧(緑線)はライン周波数の2倍の周波数(通常、欧州では100Hz、米国では120Hz)において低周波リップルを示します。
このリップルはPFC機能に固有のものです。
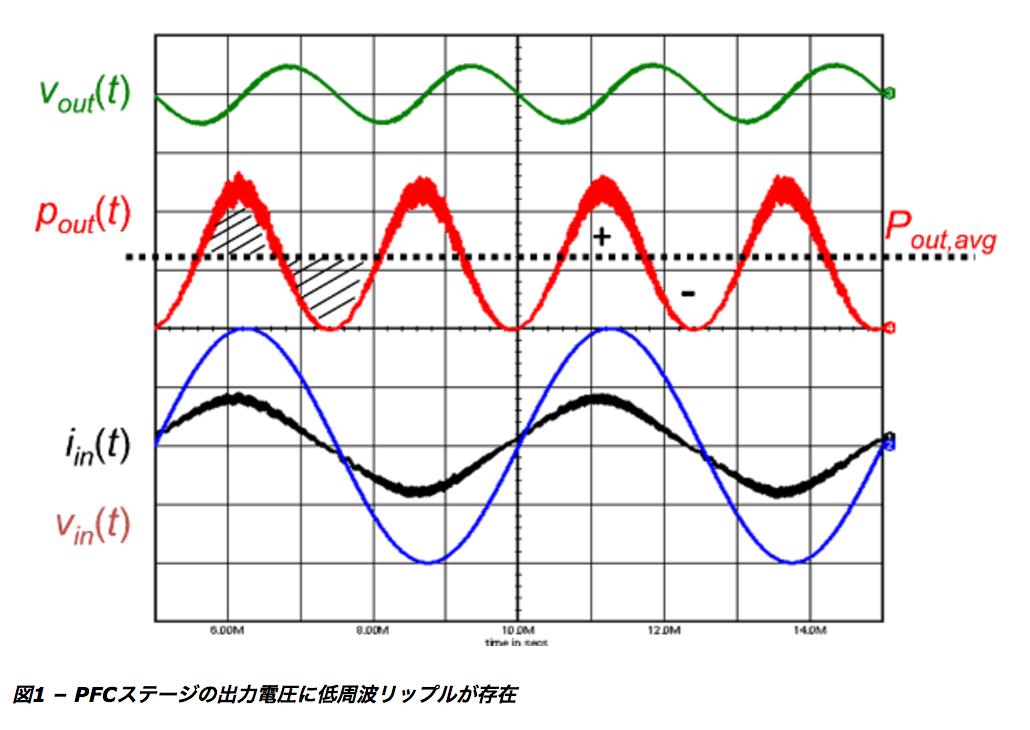
ここで、従来型の電流整形手法では、(安定化回路から供給される)制御信号をゆっくり変化する信号にする必要があります。
そうでない場合は電流が歪みます。
したがって、安定化ループは低周波出力リップルを除去することが必要です。
実際には、20Hz前後の低い帯域幅に設定してこれを実現します。
これがPFCシステムが本質的に低速システムになる理由です。
簡潔な平均化モデル
PFCステージの動特性を研究する場合、2つの異なるメカニズムが関与しており、それぞれが周波数範囲を持つと考える傾向があります。
1つは電力伝達のスイッチング・プロセスで、もう1つは入力電流整形のためにライン周波数で実行される変調です。
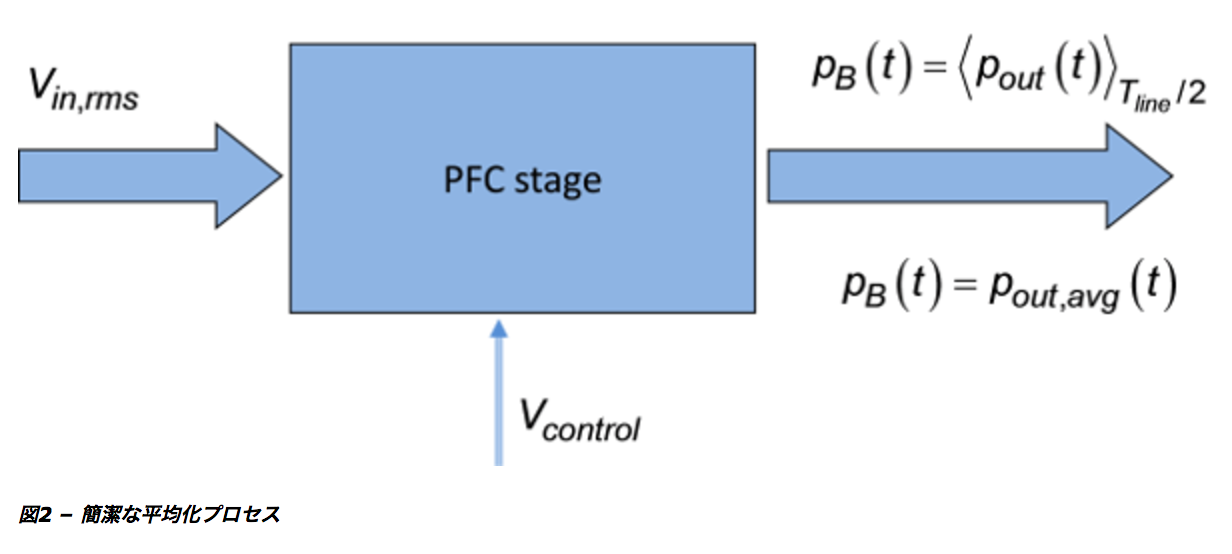
実際には、これら2つの要素を無視した簡略アプローチを使用できます。
ここで想定するPFCステージの大信号モデルは、単一ライン周期内で供給される平均電力にのみ基づくことができます。
PFCステージは、この計算した平均電力を絶えず供給するデバイスとしてモデル化されます。
スイッチング事象と入力電流整形変調は、安定して動作する発電メカニズムと見なされます。
したがって、ライン周波数より高い周波数で起こるすべての現象を無視します。
ループ帯域幅は次のとおり設定されるので、これは妥当な考え方です。
システムが臨界導通モード(CRM)ではなく連続導通モード(CCM)で、また電圧モードではなく電流モードで動作している場合、この点は問題になりません。
PFCステージから供給される平均電力のみ考慮しています。
この方法を図2に示します。
式1に、PFCステージによって供給される平均電力の一般式を示します。
電力式は、制御信号の電圧(Vcontro)とその最小値電圧((Vcontrol,min)の間の電位差によって決まります。

フィードフォワードを採用していないシステムでは、平均入力電力は2乗ライン振幅にも比例します(m=2)。
また、フィードフォワードを部分的に実装している場合は、単純にその振幅に比例します(m=1)。
一般的に、電力式は出力電圧レベルからは独立しています(n=0)。
ただし、電力がVoutに逆依存している場合は例外です。
これは何らかの連続導通モード(CCM)システムを使用している場合、つまりn=1の場合です。
NCP1605では、フォロワ・ブースト手法を採用し、電力式が出力電圧の2乗に逆比例するようにしています(n=2)。
しかし、心配には及びません。このような電力式は通常、PFCコントローラのデータシートに記載されているか、回路の動作モードが分かれば計算できます。
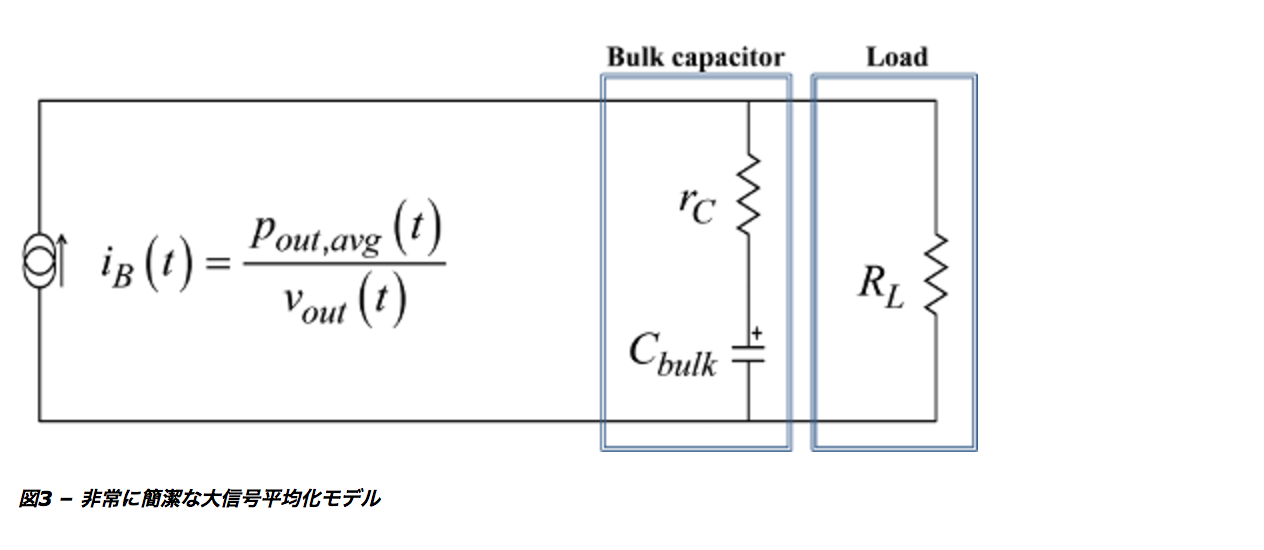
実際のところ、電力が検討を要する最良の変数とは限りません。
その代わりに、値が[pout(avg)(t)/vout(t)]の電流源iB(t)を使用します。
つまり、この電流源は出力電圧レベルを考慮して計算された電力を供給します。
ここに示す負荷は1本の抵抗(RL)と見なされます。それだけです。
このモデルを図3に示します。
伝達関数の導出
伝達関数を求めるには、小信号モデルの展開という別の作業が必要です。
これを行うには、図4に概要を示す従来式の手法を用いることになります。
最初のステップは、システム変数の小さな変動による励起が発生したときに、電流源B(t)がそのDC値付近で示す小さな変動を検討することです。
ここではライン振幅が一定と考えているので、通常、ライン変動には関心がないことに注意してください。
したがって、入力電圧の小さな変動を無視し、出力電圧(Vout)の小さな変動とVcontrolの小さな変動のみに注目します。
これらの変動がB(t)に及ぼす影響は、偏導関数を計算して求めることができます。

計算を終えると、図4の上部にある表記が得られます。
この回路は、iB and Voutに関するDC値と小さな信号変動を考慮に入れたものです。
次のステップは、小信号スケールでは何の役割もないこれらのDC値を排除することです。
VoutのAC成分による寄与を次のとおり計算することができます。

式3は、Voutの小さな変動に起因するiB vaの変動をモデル化した電流源を、1本の抵抗RL/(n+1)で置き換え可能なことを示しています。
nはPFCの電力式のうち、出力電圧による干渉を示す係数であることを思い出してください。
nは一般に0で(例えば、NCP1608が駆動するPFCステージ)、何らかのCCM PFCを使用している場合は1、NCP1605で制御している場合は2になる場合があります。
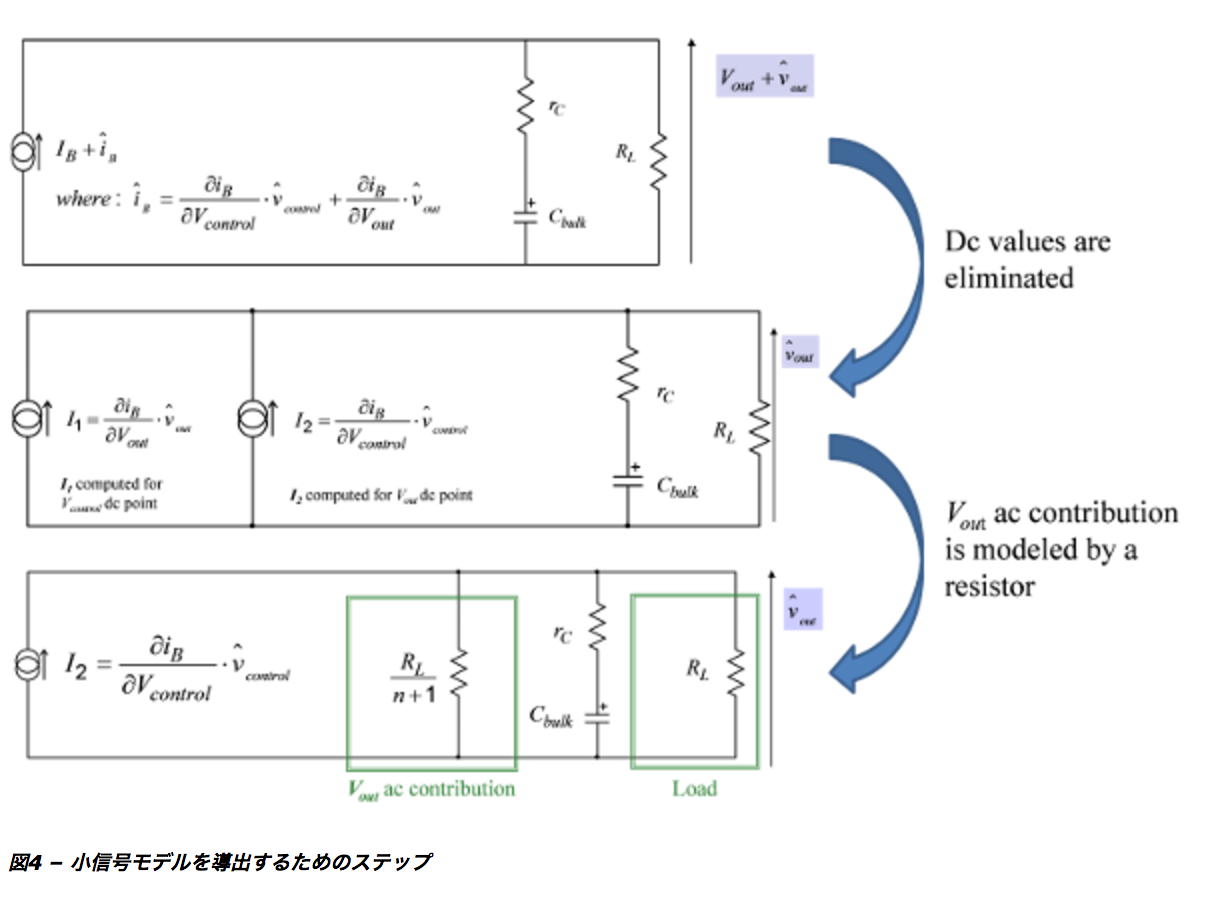
最後に、2本の並列抵抗を1本の抵抗で置き換えることができるため、図5に示す非常に簡潔なモデルが得られます。
ここで、電流源はバルク・コンデンサと並列に配置されている1本の抵抗に電力を供給します。
なお、バルク・コンデンサのESR(等価直列抵抗)であるrCを示していることに注意してください。
ただし、注目している周波数範囲(ライン周波数以下)では、このESRは何の役割も果たしていません。
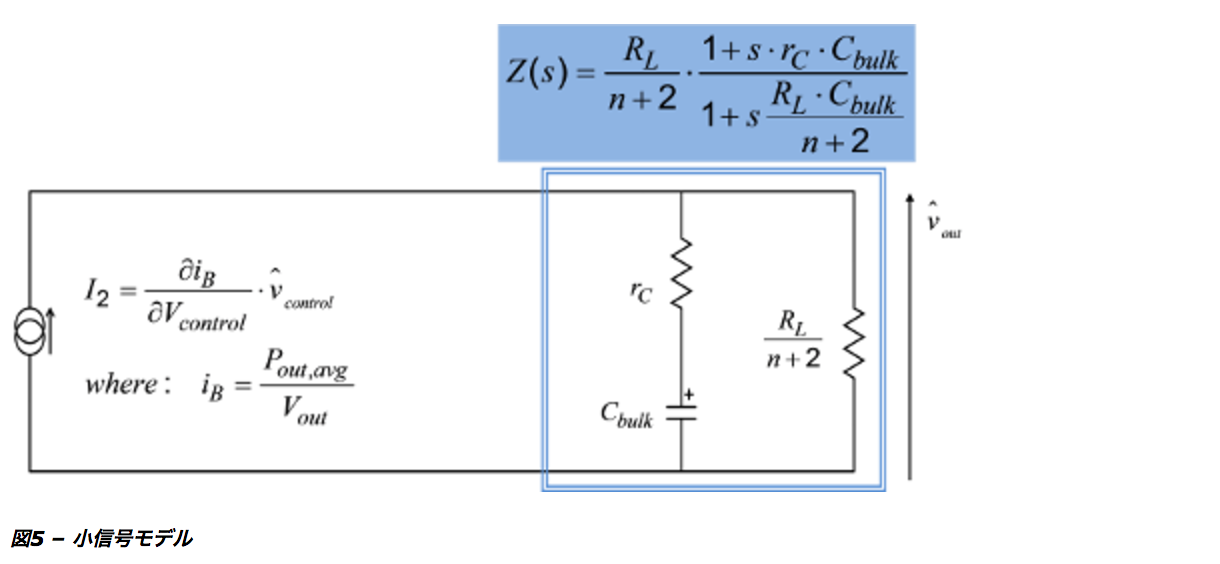
ここで、PFCステージのループを補償するのに必要な伝達関数が得られます。

NCP1654は、8ピンのCCM PFCコントローラです。
一例として、この回路で駆動されるPFCステージについて検討してみましょう。
NCP1654データシート[1]の等式16には、次の電力式が記載されています。
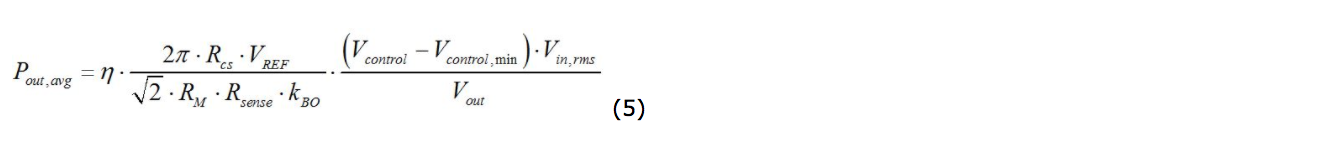
ここで、nは効率、Rcs、RM、Rsense、kBO、およびVREFはシステム定数です(Rcs、RM、およびRsenseは、最大電流レベルと最大電力レベルを設定する外部抵抗を表し、kBOは外部電圧検知ネットワークのスケールダウン係数、VREFは内部基準電圧を表す)。
NCP1654の部分フィードフォワードを使用しているので、(m=1)かつ(n=1)であることに注意してください。
これから、次の式を導くことができます。
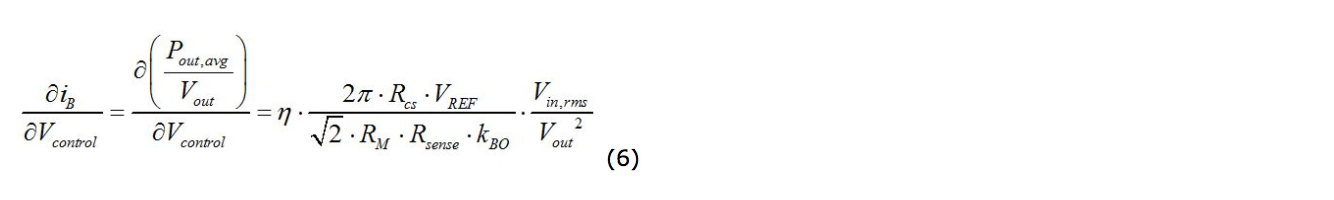
次の伝達関数を得ることができます。
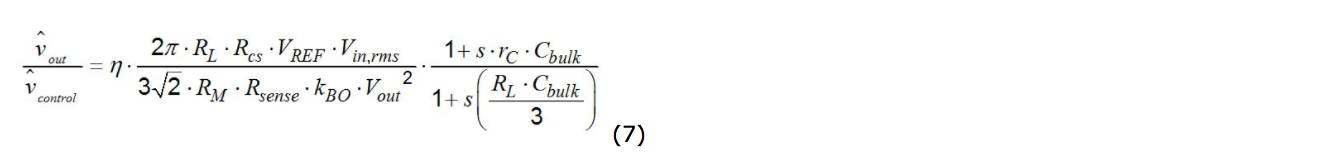
ここまで、PFCステージの出力電圧を安定化させる電圧ループ(つまり、外部ループ)のみ検討してきました。
CCM PFCには、さらに入力電流をアクティブに強制して基準正弦波に一致させるために、電流ループ(つまり、内部ループ)を実装しているものもありますが、この電流ループについては、本稿では考察していません。
出典:『PFCステージの伝達関数を素早く導き出す方法』オン・セミコンダクター