分かりにくい用語とその意味（11）振動ベクトルとポーラ線図

2012年7月号の「オービットとポーラ線図」において、ポーラ線図とは振動ベクトルを極座標上にプロットしたものでありナイキスト線図とかベクトル図とも呼ばれるとの説明をしました。

また、振動ベクトルは回転同期成分の振幅値と、そのハイスポットの位相基準に対する位相角で示されることを説明しました。

しかし、この振動解析の中でも特に理解が難しいと思われる「振動ベクトル」について、これまでの説明では不十分な部分もあり、今回は、少しでも分かりやすい解説にトライしてみたいと思います。

なお、今回の説明は長文となってしまいましたが、分割して後半を翌月見るよりも、一気に読んでいただいた方が理解しやすいかと思いますので、分割をしないで掲載させていただきました。

振動ベクトルとは

数学や物理学で一般的に取扱うベクトルとは、空間における大きさと方向を持った量ということで理解されます。

振動ベクトルも「振幅値」という大きさと「位相角」という方向を持った量ということになりますが、それは実際の空間に対して静止した座標上で観測したものではなく、回転するロータに同期して回転する座標上で観測した大きさと方向ということになります。

この静止した空間におけるベクトルではないというところが理解しにくい点ではないかと思いますので、以下に順序立てて説明を進めたいと思います。

説明モデルの前提条件

できるだけ考えやすく、分かりやすくするため、下記のように単純化したモデルを説明の前提条件とします。

ポーラ線図における真上の方向（天の方向）を振動ベクトルの 0（ゼロ）度として、回転方向とは逆方向に角度を取っていく。

つまり、回転方向より遅れ方向をプラス（+）、進み方向をマイナス（-）とする。

単純にするために、ロータ上の位相基準マークとして取付けられた切欠き状のキー溝を検知する位相基準センサの取付角度を実際の空間における真上の方向（天の方向）で 0 度として、ロータの振動変位を測定する変位センサの取付角度も実際の空間における真上の方向（天の方向）で 0 度とする。

また、測定対象となるロータは、両端を軸受で支持された質量が無視できる回転軸の中央に質量を有する1つの円板が取付けられた理想的なロータ（いわゆるジェフコットロータ）であり、軸振動としては不釣合いによる調和振動のみ発生するものとする。

つまり、回転同期成分（1X）の振動のみ発生するロータを対象として考える。

回転機械の振動ベクトルとは？

ここでは回転機械の回転構成部品を含むロータの振動ベクトルについて議論します。

それは、回転軸中心と質量中心（重心）のずれを持つロータが回転運動することによって励起される加振力の結果としてロータの振動変位に現れる位相基準に対する方向と大きさということになります。

この加振力以外の力が加わらない状態において、回転数が一定の時、この振動変位の静止した空間における振れ回りの方向は、回転に同期して回転します。つまりロータが回転に同期して振れ回っている状態です。

ここで、振動ベクトルの方向というのは、実際の静止した空間における振動変位の振れ回る方向のことではありませんのでご注意ください。

実際の静止した空間における軸の挙動

実際の静止した空間から回転するロータを観測した場合、その軸はどのような挙動を示すのでしょうか。

図 14 は、一定回転数で回転している軸において、位相基準が静止した空間上の真上に来た時点を初期として、そこから 1 回転する間を、1/8 回転毎（45 度毎）に（a）〜（i）の順で示したものです。

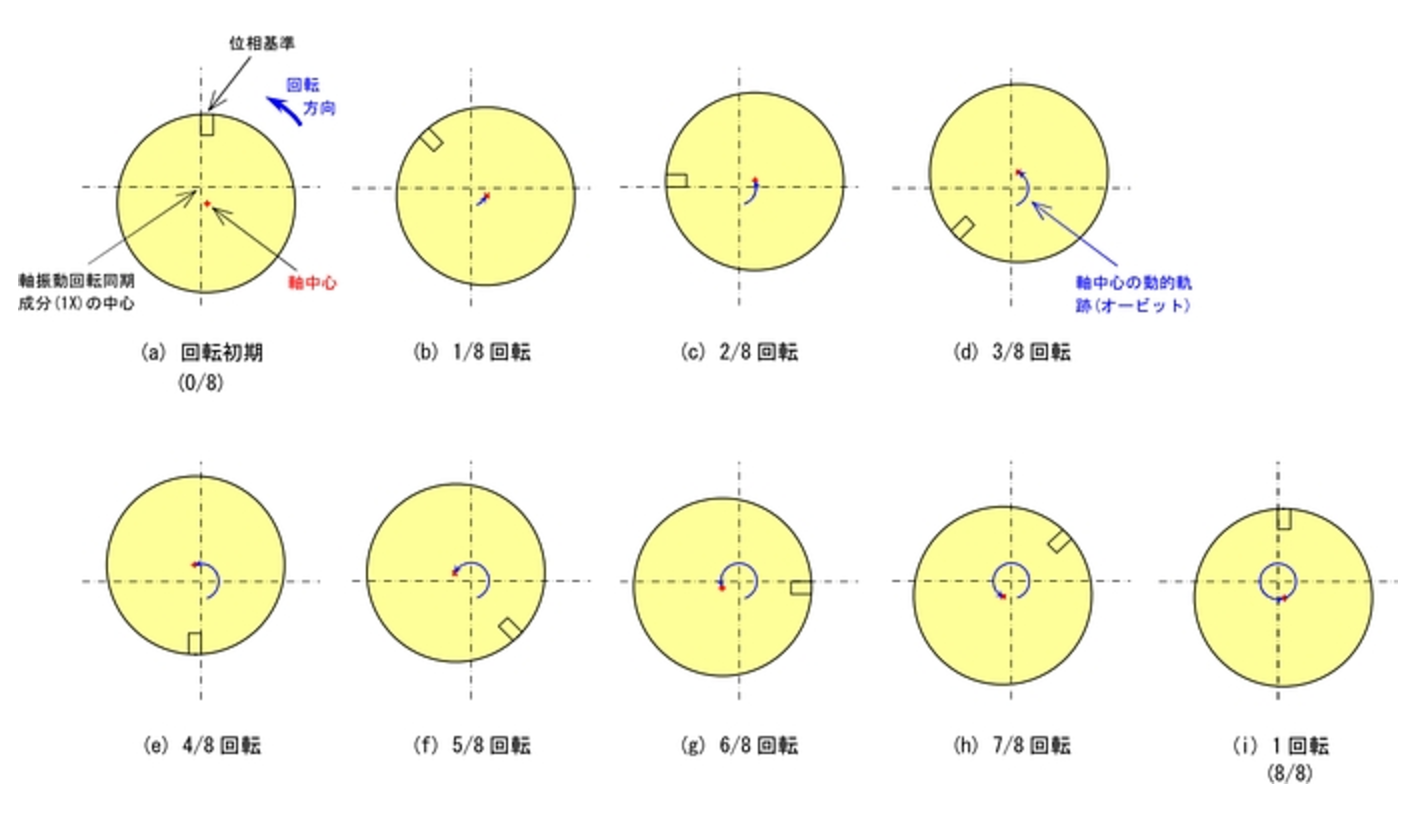
▲図14.実際の静止した空間上の座標から見た軸振動における軸の挙動

この例では、真上に位相基準が来る時＜（a）と（i）＞、軸中心のダイナミックな軌跡であるオービットの中心（一点差線で示した水平軸と垂直軸の交点）に対して、軸中心が右下の方向、真上を0度とすると約 160 度の遅れ方向にあることが分かります。

これを真上に取付けられた変位センサで測定すると、位相基準が通過してから約 160 度遅れたところ（約 3.5/8 回転）、つまり図（d）と（e）の間で最もロータがセンサに接近し、約 340 度遅れたところ（約 7.5/8 回転）、つまり図（h）〜（i）の間で最もロータがセンサから離れた状態を繰り返すことになります。

この時、変位センサとして FK-202F のような、感度がマイナスでギャップ増大とともに出力電圧が減少するような変位センサを適用している場合、その出力波形は図 15 の（a）に示すようにロータの上下をそのまま反映して、ロータが最も上に動いてセンサに最も接近したところが波形のピークで、ロータが最も下に動いてセンサから最も遠ざかったところが波形のボトムとなるような正弦波となります。

ここで、波形のピークの点、つまり振れ回っているロータが最も上に動いて変位センサに最も接近した点を「ハイスポット」と呼びます。

図 15 に示すように、振動ベクトルの大きさは振幅Aで示し、振動ベクトルの方向は、ロータの 1 回転を 360 度として、位相基準とハイスポットの角度差、つまり位相角 θ で示します。

これをポーラ線図に展開すると図 15（b）の赤い点で示す位置にプロットされます。

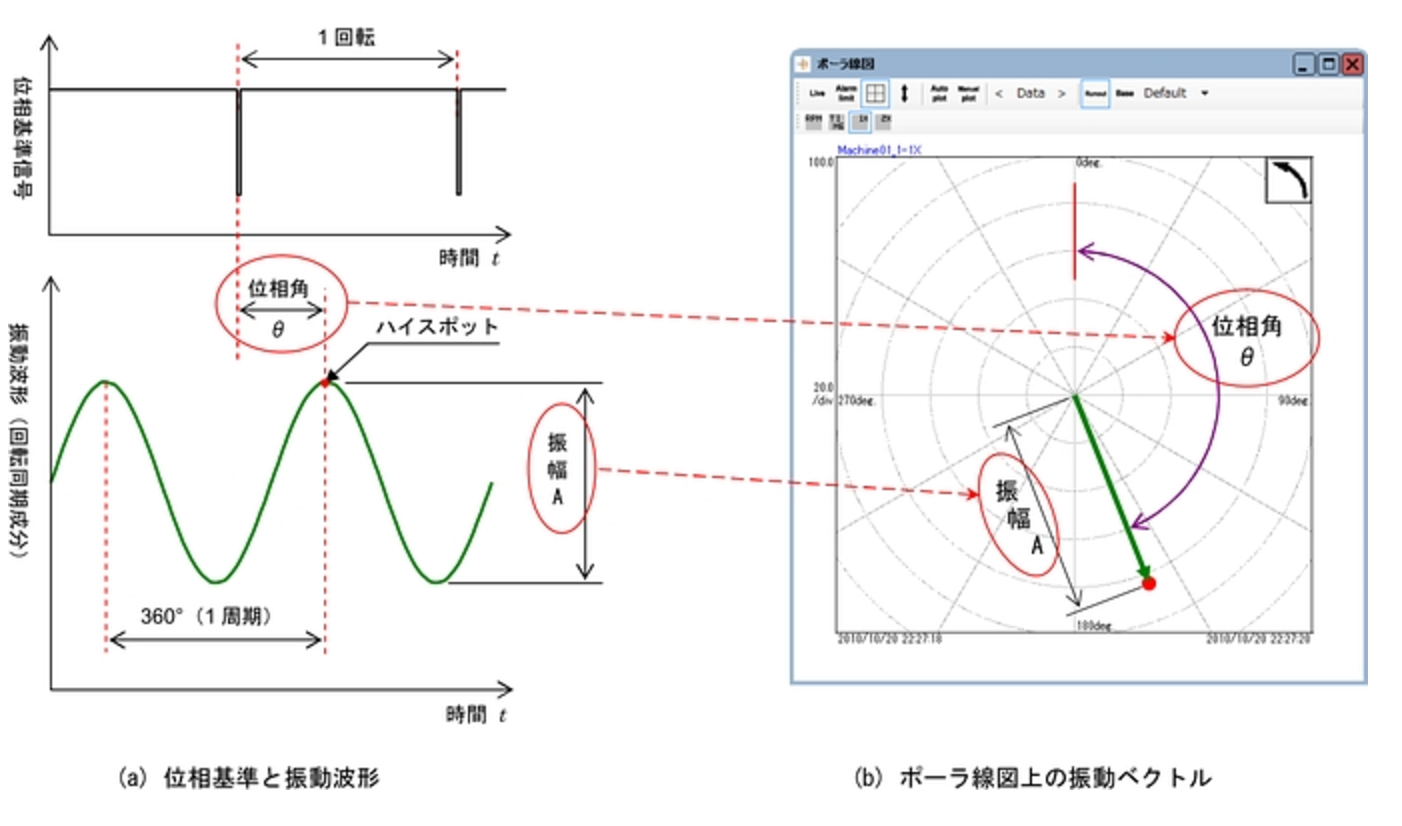
▲図15. 振動波形における振幅と位相角およびポーラ線図の振動ベクトルの関係

ロータの回転に同期して回転する座標での観測

上記の図 14 と図 15 による説明は、ロータの軸振動における位相基準と振動波形の関係、そこから示される振動ベクトルの大きさと方向を示していますが、感覚的には分かりにくいかもしれません。

そこで、図 14 のようにロータが回転している時、私達が観測する座標軸も回転に同期して一緒に回転させてみましょう。

その時、ロータの位相基準を 0 度として、位相角は回転方向とは逆方向に角度を取って行くこととします。

図 16 は、図 14 で示した一定回転数で回転するロータに対して、オービットの中心を原点とする、ロータの回転に同期して回転する座標軸を位相基準が静止した空間上の真上に来た時点を初期として、そこから 1 回転する間を、1/8 回転毎（45 度毎）に（a）〜（i）の順で示したものです。

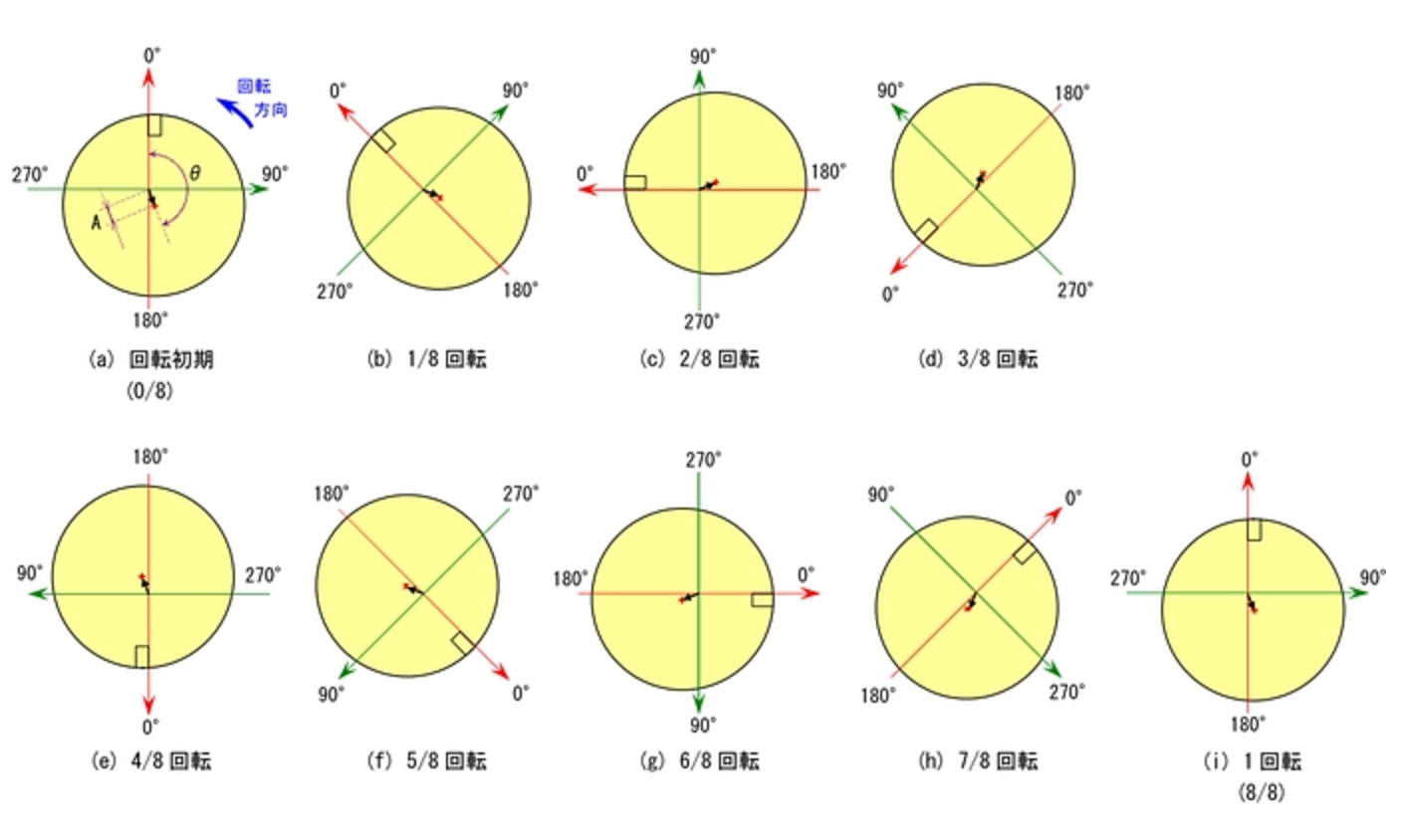
▲図16. ロータの回転に同期して回転する座標から見た軸振動における軸の挙動

今、私たちはこのロータの回転に同期して回転する座標軸の上に乗ってロータを観測しているわけですから、ロータは静止して（回転していないように）見えます。

この座標軸が振動ベクトルを表示する座標、つまりポーラ線図（またはベクトル図、ナイキスト線図）の座標と同じものを示していると考えられます。

この座標上ではロータは位相基準を真上（0 度）に向けて、軸中心が座標の原点からいくらかずれた状態として見ることができます。

ここで、座標の原点から軸中心に向けて矢印を引いてみましょう。

これが振動ベクトルです。

図 16 に示すように、この座標軸における軸中心の位置は、（a）〜（i）の全ての過程で同じ位置を示しており、一定の回転の中では振動ベクトルも一定であることを示しています。

つまり、振動ベクトルは回転しているロータを、回転に同期して観測して、静止させて見えるようにした場合の偏心量とその方向ということになります。

ここで観測される偏心量は、静止した空間においては、その変位分だけ偏心して回転しているわけですから、軸振動の大きさである振幅を表すことが理解できると思います。

なお、お気付きのように、ここで観測する偏心量（ベクトルの長さ）は、片振幅の大きさと等しい値になりますが、便宜上、振動ベクトルを表すポーラ線図上では振動値は両振幅で表示しています。

上記のように、振動ベクトルはロータの回転に同期した座標軸上で観測した偏心の量と方向であると考えることができます。

余談ですが、よく勘違いされることのあるオービットは静止した座標軸上（つまり実際の空間上）で観測した動的な軸中心の軌跡であり、観測者の座標が全く異なるということが理解していただけると思います。

今回説明した振動ベクトルに関しては、さらにハイスポットとヘビースポットの関係や、バランシングへの適用等も理解していただきたいと思いますので、次回はそのあたりの説明をしていきたいと思います。

出典：『技術コラム回転機械の状態監視や解析診断』新川電機株式会社