分かりにくい用語とその意味(12)ハイスポットとヘビースポットの位相角
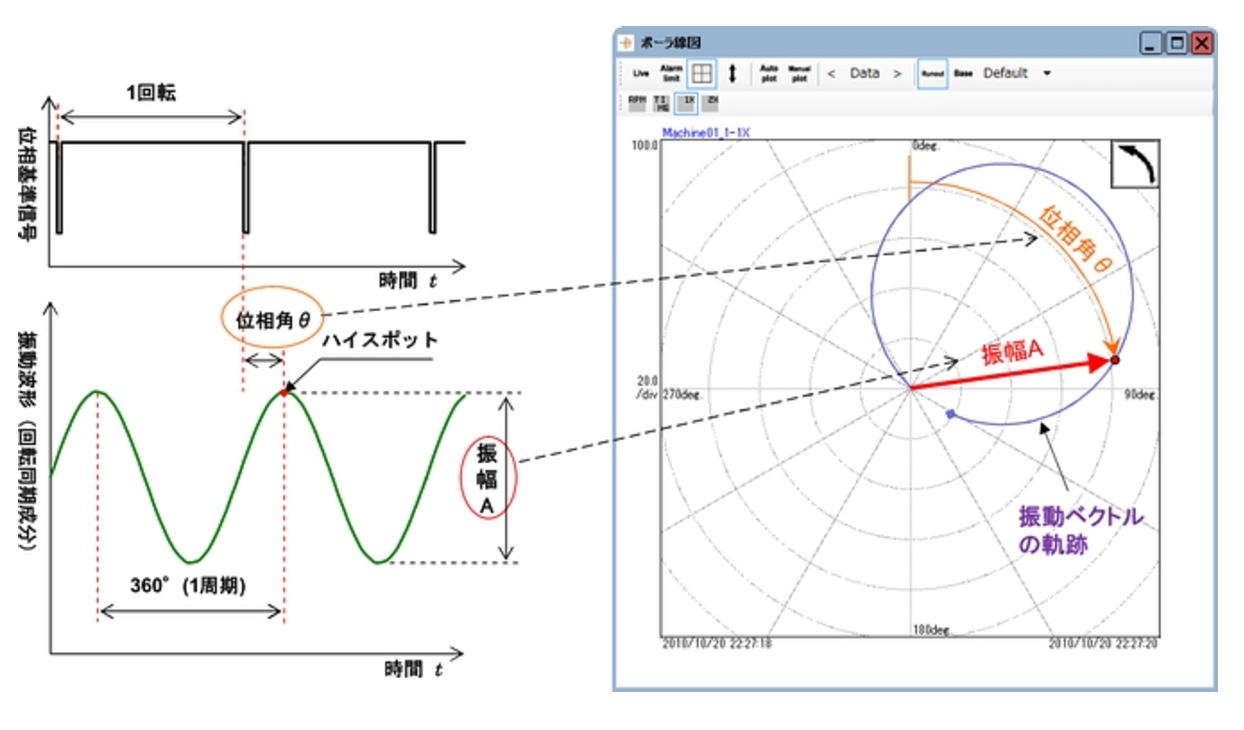
前回は、位相基準センサと変位センサが実際の空間における真上の方向に取付けられている場合、振動波形のピークの点、つまり振れ回っているロータが最も上の方向に動いて、変位センサに最も接近した点を「ハイスポット」と呼び、その時の振幅 A が振動ベクトルの大きさ、位相基準とハイスポットの角度差が振動ベクトルの方向を示す位相角 θ として、ポーラ線図上に示されることを説明しました。
今回は、このハイスポットとヘビースポット(重心点)の関係について説明します。
説明モデルの前提条件は前回と同様に下記の通りとします。
説明モデルの前提条件
できるだけ考えやすく、分かりやすくするため、下記のように単純化したモデルを説明の前提条件とします。
ポーラ線図における真上の方向(天の方向)を振動ベクトルの 0(ゼロ)度として、回転方向とは逆方向に角度を取っていく。
つまり、回転方向より遅れ方向をプラス(+)、進み方向をマイナス(-)とする。
単純にするために、ロータ上の位相基準マークとして取付けられた切欠き状のキー溝を検知する位相基準センサの取付角度を実際の空間における真上の方向(天の方向)で 0 度として、ロータの振動変位を測定する変位センサの取付角度も実際の空間における真上の方向(天の方向)で 0 度とする。
また、測定対象となるロータは、両端を軸受で支持された質量が無視できる回転軸の中央に質量を有する1つの円板が取付けられた理想的なロータ(いわゆるジェフコットロータ)であり、軸振動としては不釣合いによる調和振動のみ発生するものとする。
つまり、回転同期成分(1X)の振動のみ発生するロータを対象として考える。
ハイスポットとヘビースポットの位相角
ロータを軸方向から見た場合、ロータの中心点と、そのロータの質量の中心である重心点、つまりヘビースポットが完全に一致していれば、ロータを回転させても振動は発生しません。
しかし、ロータの中心点とヘビースポットが一致していない場合、つまり重心の偏りである不釣合いがある状態でロータを回転させると、ヘビースポットの遠心力により、ロータに振れ回り振動を励起させるような加振力が発生し、ロータが振動することになります。
この不釣合いによる振れ回り振動を抑えるためには、ロータの中心点に対してヘビースポットと反対方向に適当なおもりを付加して、ロータのバランスを取ることが必要となります。
そこで、ヘビースポットの位置と大きさが分かればよいのですが、これは単純に振動を測定していても分かりません。
そこで、まずハイスポットの位置や大きさ、つまり振動ベクトルとヘビースポットの位置との関係を考えてみましょう。
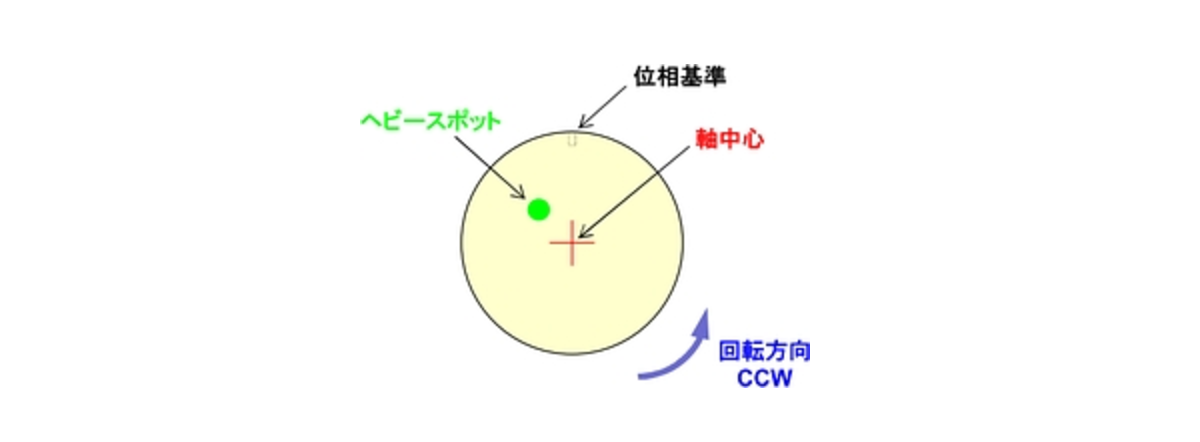
図 17 に示すようなロータの中心点とヘビースポットの位置が一致していない、不釣合いを持つロータを考えてみます。
ここでは仮に、ヘビースポットの方向が位相基準よりも 45° 回転進み方向にあったとします。
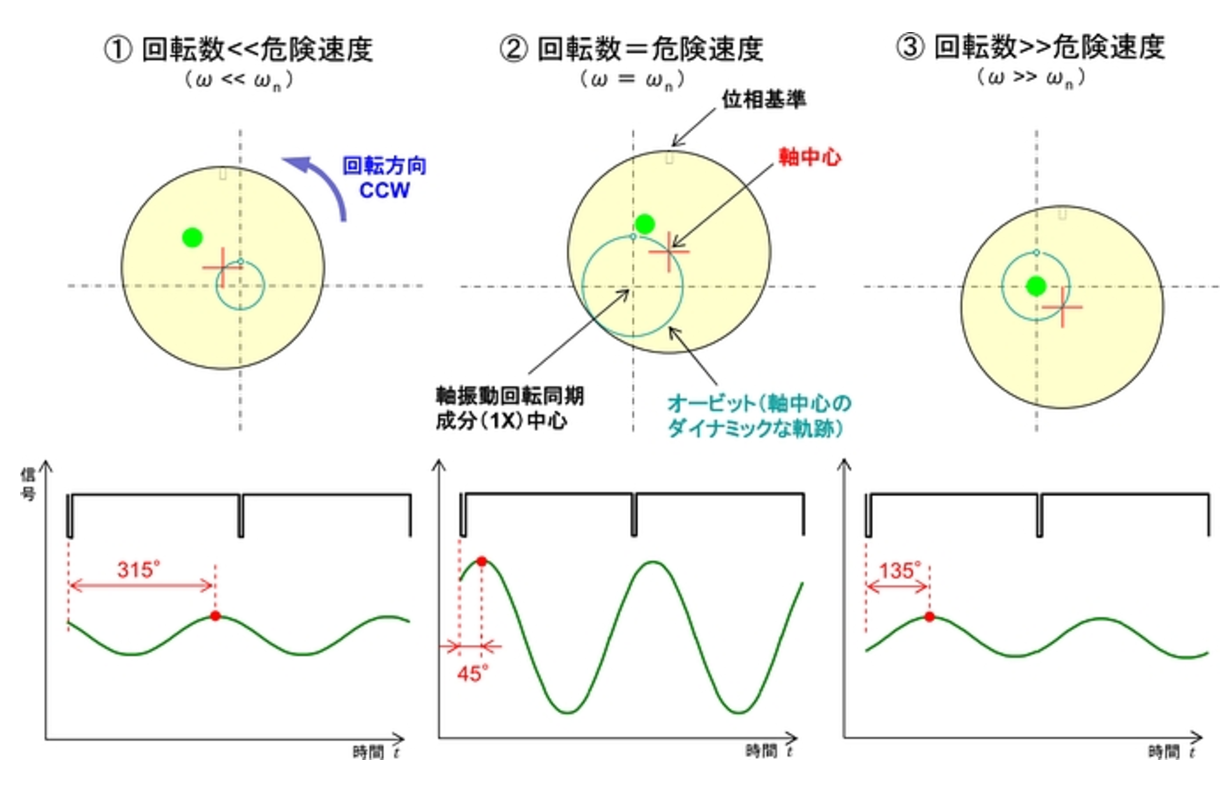
このロータを回転させた時の状態を図 18 に示します。
まず、ロータの回転数が危険速度に比べて十分に低い場合(ω≪ωn)、図 18 ① に示すように、ロータはヘビースポットの方向に引っ張られる形で振れ回り、ヘビースポットとハイスポットはほぼ同じ方向、つまりヘビースポットの方向と振動ベクトルの位相角はほぼ同じとなります。
このモデルでは、ヘビースポットの方向が位相基準よりも 45° 進み方向にあるものとしていますので、回転方向とは逆の遅れ方向に角度をとる位相角はほぼ 315° ということになります。
次に、回転数が上昇して危険速度に到達した場合(ω=ωn)、図 18 ② に示すように、ロータはヘビースポットの方向から 90° 遅れた方向にピークを持つような振れ回り運動をしますので、位相角は ① の状態からもほぼ90°遅れた状態となります。
したがって、このロータでの危険速度における位相角は 315+90=405° 、つまり 45° ということになります。
最後に、さらに回転数が上昇して、危険速度に比べて十分に高い場合(ω≫ωn)、図 18 ③ に示すように、ロータはヘビースポットの方向から 180° 遅れた方向にピークを持つような振れ回り運動をしますので、位相角は ② の状態からさらにほぼ 90° 遅れた状態となります。
したがって、この状態での位相角は 45+90=135° ということになります。
このように、ロータは危険速度より低い回転数では、回転数上昇とともに位相角が遅れていき、振動振幅が上昇し、危険速度では位相角が初期位相から 90° 遅れるとともに最大振幅となります。
危険速度を超えてさらに回転数を上昇させていくと、さらに位相角が初期位相から 180° に向けて遅れていき、振動振幅は減少していきます。
この様子をポーラ線図上にプロットすると、その軌跡は図 19 と図 20 に示すようになります。
▲図19. 回転数変化に伴うポーラ線図上の振動ベクトルの軌跡
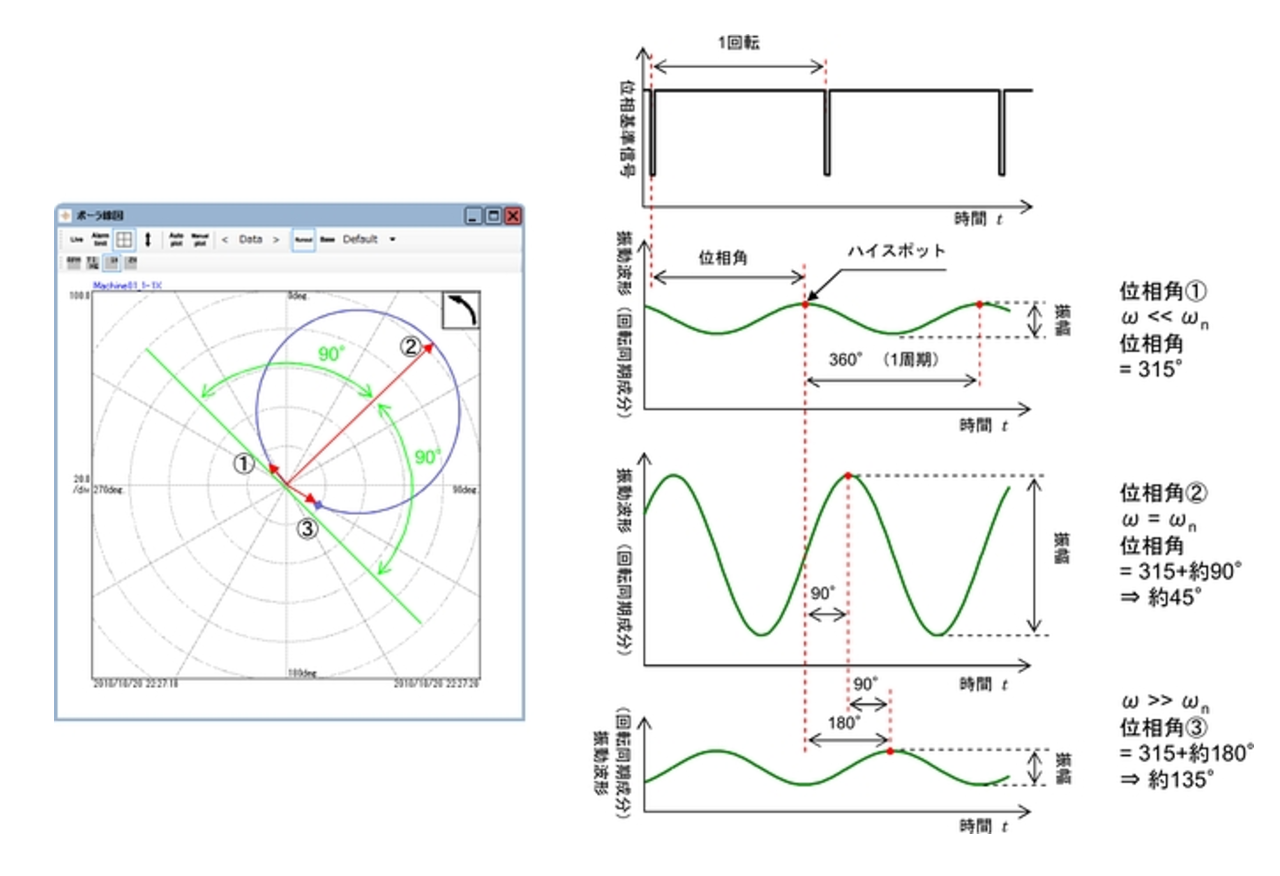
▲図20. 回転数変化に伴うポーラ線図上の振動ベクトルの軌跡と波形
図 20 を見ると、ヘビースポットの方向は、危険速度における振動ベクトル ② の位相角から 90° 進み方向にあるということが分かります。
したがって、ロータの回転数を低速回転から 1 次の危険速度を超える高速回転数範囲まで変化させて、ポーラ線図上で振動ベクトルの軌跡をプロットすることができれば、ロータ上のどの方向にヘビースポットがあるのかが分かります。
そうすると、ロータの中心点に対してヘビースポットと反対方向に適当なおもりを付加して、ロータのバランスをとればよいという事になりますが……。
しかし、これだけではおもりの質量をいくらにするのが適当な値という事になるのかは分かりません。
また、危険速度を超えることなく、停止状態から一気に定格回転数に到達するようなロータで、ある一定の回転数での振動ベクトルしか計測できないような場合、ヘビースポットの方向さえ知ることができません。
そこで次回は、試しおもり付加してバランス調整を行う方法について説明します。
出典:『技術コラム 回転機械の状態監視や解析診断』新川電機株式会社