『改善ぷちセミナー』問題解決アプローチ
※当コンテンツは『面白狩り』の提供でお届けいたします。
1.効率的な問題解決
今回のお話は、改善活動には役には立たないかもしれません。が、改善のウンチクを身に付けるつもりで知っておけば、迷った時のヒントになるかもしれません。
気楽に読んでください。
苦しい経営をやりくりしている会社は、早く問題を解決して経営を立て直さなければいけません。
たとえ、順風満帆に利益を生みだしている会社でも、周囲の経営環境はどんどんレベルアップしていきますから、何もしないでいたらすぐに取り残されてしまいます。
問題解決には終わりがありません。問題解決を怠らず、常に進歩していく、それがビジネスです(世の中ご覧なさい。それができない、あるいはしない組織は必ず腐って、破綻しています)。

ただし、問題を解決するのに、思考錯誤に時間がかかって期待したほどの結果も出ないのでは困ります。
合理的に要領よく進めることが、重要になってきます。
合理的というのは、理に適っているということです。つまり、論理的に考えて行うということです。
よく改善の参考書などでは、論理学に基づいた問題解決アプローチについて説明されています。
ところが、この手の話をマジでやろうとすると(本当は面白いんですけどね)理屈っぽくなって、何が何だかわからなくなってしまいます。
そこで、要点だけ簡単にお話します。
2.問題という概念
みなさんが改善活動を進めるときは、目の前にある障害や困難に気付いて、それらが解消できたら良しとします。
このとき、その成果は、必ず金額で評価されなければなりません。
……なんて言い方をすると、守銭奴のように感じるかもしれませんが、ビジネスである以上はそうでなければなりません。したがって、問題という概念もコストで考えなければなりません。
問題とは何か?……については、別のコンテンツ(『品質でもうけなさい』1.問題のない会社はもうからない)でも触れているので、ここではくどくどお話しません。
問題とは理想と現実との差(ギャップ)です。

現実というのは、たくさんのムダが含まれているために、大きなコストになっている現在の状態です。
これに対して、理想とはムダが排除されてコストが削減された状態です。
コストの大きさを横軸にとって問題を考えると、下のような三角形になります。
三角形の底辺が現実のコストです。また、コストが小さければ小さいほど良いわけですから、コストゼロである頂点が理屈の上では理想ということになります。
実際にはコストゼロなんてあり得ないことなので、もっと下のあたりに実現可能な理想があります。
実現可能といっても、実際には初期コストや導入期間にムリがあることが多いので、さらに下がったところに現実的な理想の姿があります。これが最適システムで、いわゆる「あるべき姿」です。
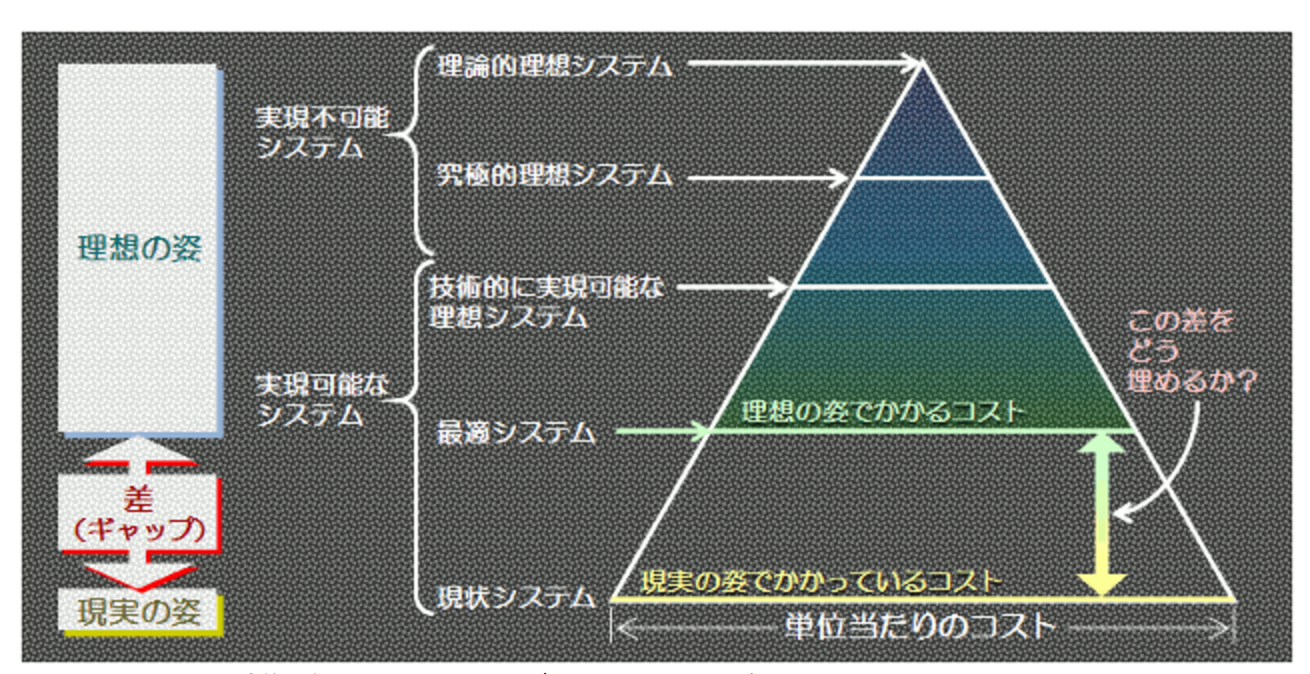
※1.理論的理想システム:コストゼロのシステムで現実にはありえない
※2.究極的理想システム:現在は不可能だが、科学の発達や新技術開発によって実現可能な姿
※3.技術的に実現可能な理想システム:資金上の制約や量的な制限などさえなければ実現可能な姿
※4.最適システム:現状の実態に適合した理想の姿。いわゆる「あるべき姿」
※5.現状システム:現在のシステム。たくさんのムダが含まれている。
最適システムの位置は技術革新によって上がっていきます。コスト削減だけを考えれば、人件費や税金の安い場所に生産拠点を移すなども手段の一つです。
しかし、そのような小手先のやり方で最適システムのところに到達したところで、そこ止まりです。
そこで足踏みをしている内に、どんどん周囲に取り残されていくわけです。技術革新とそれを支える改善活動が大切なのはこういうことです。
3.代表的な問題解決アプローチ
問題解決の目標は、最終的にあるべき姿を実現することです。
古くからさまざまな方法で進められ、それらの中には手法・技法として確立されたものもあります。
こうした問題解決の進め方は、分析型と設計型という2つのアプローチに大別することができます。
(1)分析型問題解決アプローチ
分析型アプローチは、まず現状調査を行って、それを基に問題点を見出して是正するという、最も一般的な方法です。
みなさんもよく知っているQCやIEがその代表的なものです。
上のコスト三角形で見れば、底辺から問題解決の成果を積み上げていって、最適システムに近づけようという進め方です。

破線が問題解決を行った後の状態を示しています。
問題の対象が持つ条件によって、大きな成果になることもあれば、あまり成果が得られないこともあるために、このようにデコボコになっています。
例えば、ある改善活動が大きな成果を挙げても、他に問題が解決していない部分があるために、全体としての成果になっていないということがよく起こります。
これが部分最適化で、分析型アプローチの短所になっています。
とはいえ、分析型アプローチはわかりやすくて、いかにも改善活動をやっている実感があるので、小集団活動や改善提案などで身近な問題解決を行う場合に適しています。
(2)設計型問題解決アプローチ
設計型アプローチは、分析型とは逆に、まずあるべき姿を理論から見出し、これに対する現実の制約を調査して、代替案をくり返しながら実現を目指していく方法です。
VEやワークデザインが代表的なものです。上のコスト三角形で見れば、理想システムから始めて、技術的限界や制約条件を確認しながら目標を下げていって、最適システムに近づけようという進め方です。
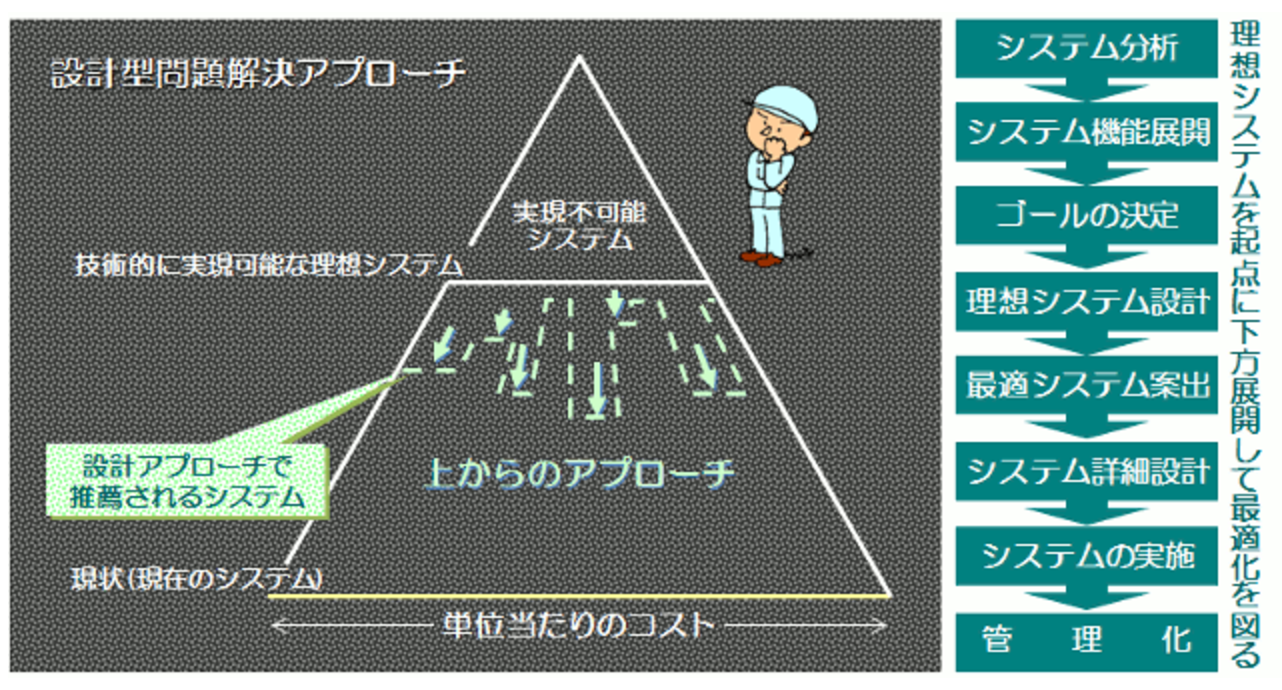
破線が代替案をくり返した後の目標を示しています。分析型による成果と同様のデコボコになります。
この場合も、どんなにハイレベルなシステムが可能でも、部分最適になってしまいますから、全体としてのシステムは低いレベルに合わせることになります。
ただし、その最低線が最適システムであれば良いので、後はそれを目標として全体をレベルアップします。
このように全体最適化ができるので、新製品開発の他、ライン編成や管理システムの構築など大きな改革プロジェクトに向いています。
半面、まず理論から始めるために机上論に陥りやすく、非現実的な問題解決になってしまう危険性があります。
この2つのアプローチを並べて比較すると、こんなふうです。
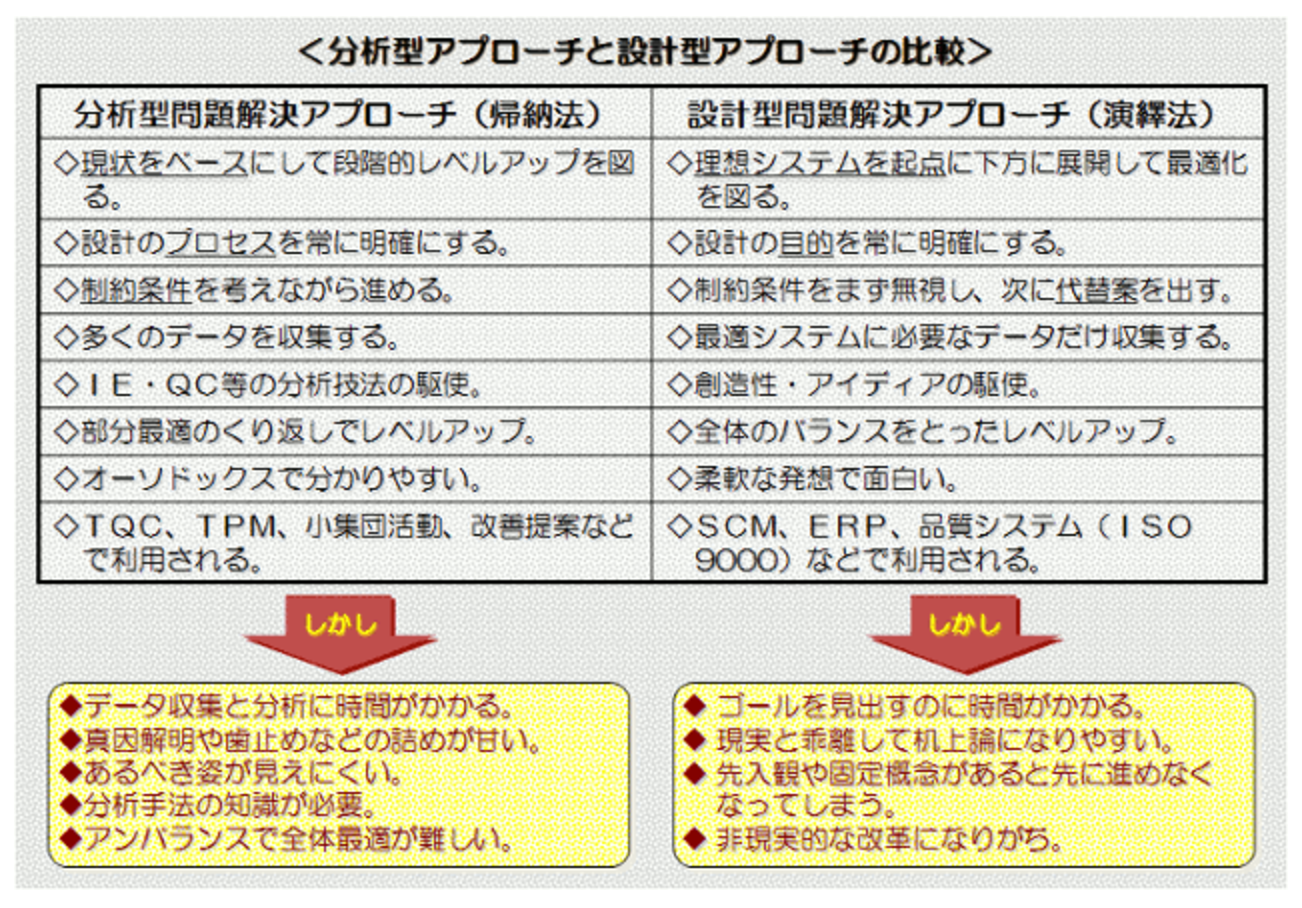
4.基本的な論理思考
分析型アプローチと設計型アプローチは、それぞれ帰納的アプローチ、演繹的アプローチとも呼ばれます。
この、帰納的、演繹的というのは、論理学で古くから知られている帰納法と演繹法という2つの基本的な論理思考によります。
帰納法(Inductionインダクション)は、まず個々の事実や特殊な問題を踏まえて、それを拡張して一般的で普遍的な理論や規則を見出そうとする考え方です(拡張的推論)。

演繹法(Deductionディダクション)は、公理とか定理、規則のような普遍的あるいは一般的な理論を前提にして、個々の事実や特殊な問題を解明していく考え方です(解明的推論)。

要するに、まず事実があってそれから理論を見出そうとするのが帰納法、まず理論があってそれから事実を解明しようとするのが演繹法です。
生産現場などで実際にありそうな問題で比較してみましょう。
例1.ある機械の動力ユニットの駆動部が鉄サビでロックしてしまった……という不具合が起きた。
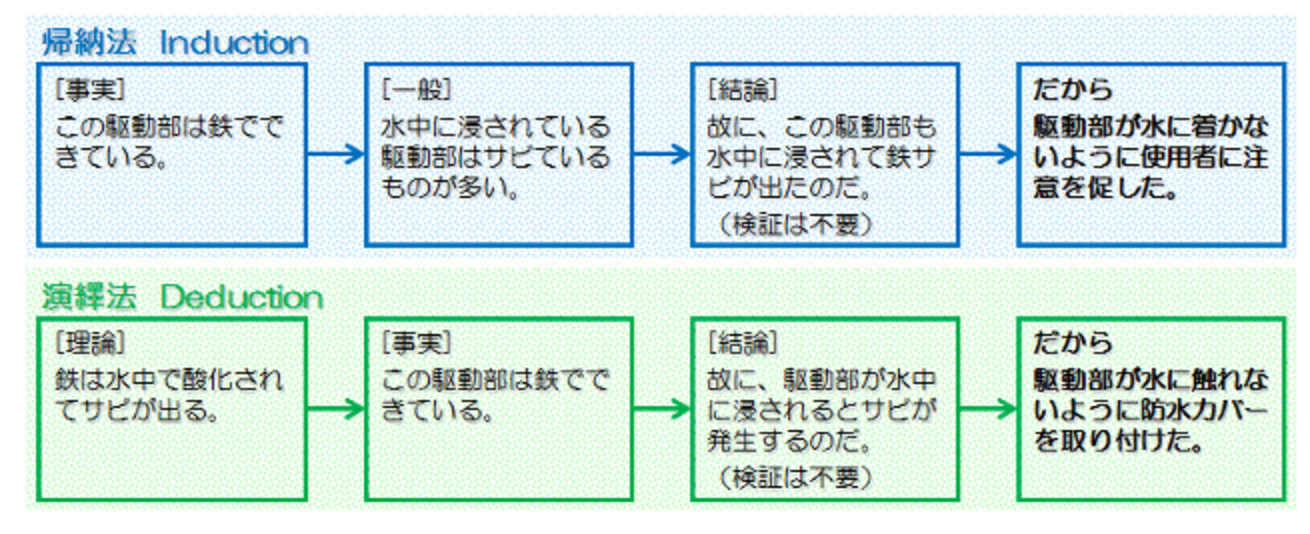
例2.納入した製品ロットの中に異品が混入した……という不具合が起きた。
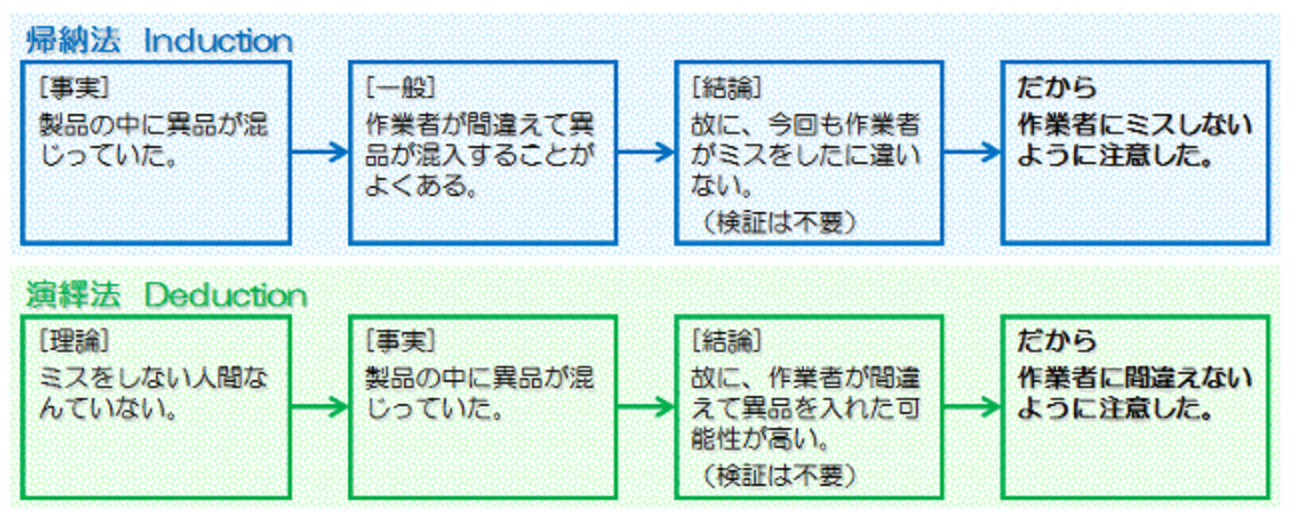
いずれも、結論後の検証が不要なのは、結論を導く前に事実の調査を行っているからです。
その調査に時間と手間がかかるので、問題解決の場合は計画的にやることがとても大切になります。
小さな改善でも、事前にガントチャートやフローチャートを作ってプランニングするのはこのためです。
5.第三のアプローチ
その場しのぎの無手勝流で迷路に迷い込んだ挙句に挫折してしまうくらいなら、多少面倒でも合理的なやり方できちんと結果を出す方が良いに決まっています。
ところが、帰納法も演繹法も合理的ではありますが、要領よく……ということになると、いずれも結論を得るまでに時間がかかるという欠点があります。
そのために、結論を急いで対策が決め打ちになりがちです。効率的に問題解決を行うために、この欠点を解消する考え方はないものでしょうか。
実は、論理学では帰納法・演繹法の他にもう一つ、仮説設定法(Abductionアブダクション)という思考パターンがあります。
これは、問題に関する一般的な事象と理論に基づいて、問題を最も適切に説明しうる仮説を導き出そうというものです(発見)。

上の2つの例を考えてみると、
例1.ある機械の動力ユニットの駆動部が鉄サビでロックしてしまった……という不具合が起きた。

例2.納入した製品ロットの中に異品が混入した……という不具合が起きた。

仮説設定法の場合、結論からすぐに対策を取ることはできません。というのは、この仮説が正しいかどうかの検証が必要だからです。
なぜ、仮説までしか導かないこの思考に注目するかというと、一般的事象と理論の調査を上手に行えば、早い段階で正解に近い仮説を導くことができるからです。
また、帰納法や演繹法のような広範囲な調査ではなく、仮説に的を絞った検証をすれば良いからです。
上手に行うとは、問題解決の経験豊富な第三者から意見やアドバイスをもらいながら進めることです。
ゼロから始めるより、一般的事象や理論についての経験と知見を持っている人の力を借りた方が、早く結論に達することができます。例えば、コンサルタント、社内や取引先のベテラン実務者の他、いわゆるオタク族も使いようによっては思いもよらぬ大きな力になります。
帰納法がコスト三角形の下からのアプローチ、演繹法が上からのアプローチとすると、仮説設定法は横からのアプローチ、経験豊富なマンパワーの活用というイメージです。これを仮説検証型問題解決アプローチと呼ぶことにします。
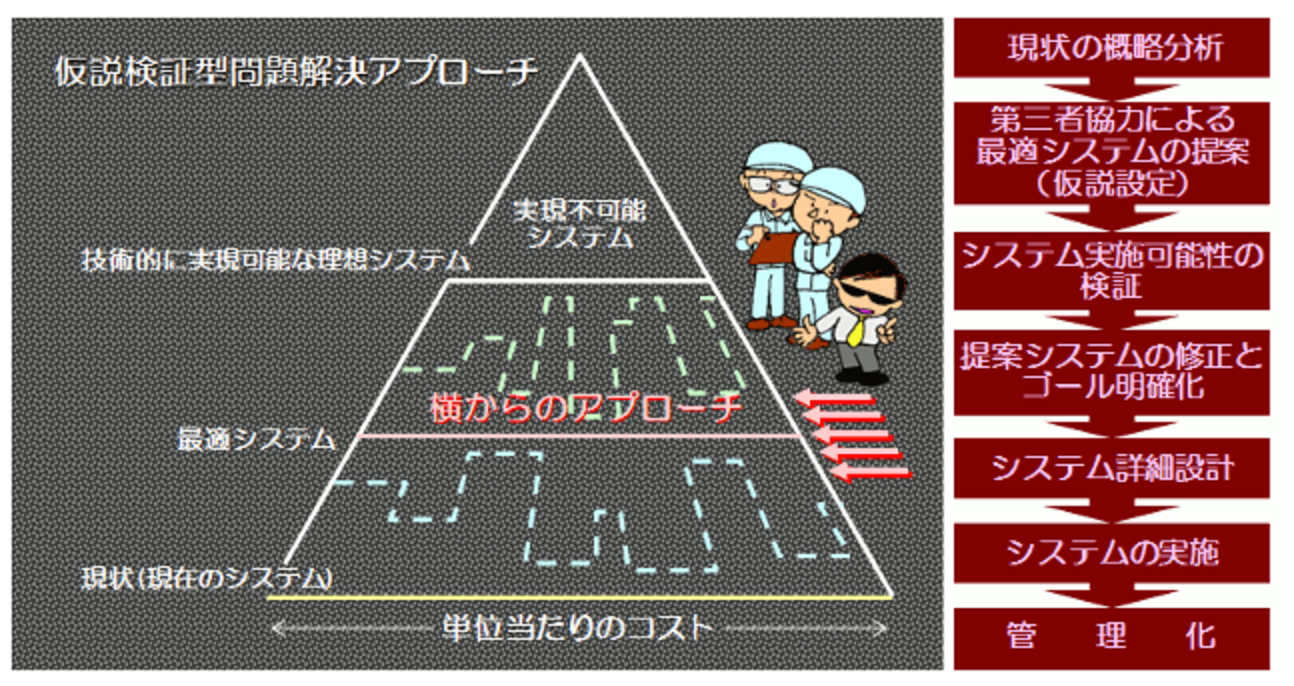
仮説検証型アプローチは私の個人的な提案に過ぎません。しかし、決して新しいアプローチなのではなく、実は古くから行われていた方法です。
昔は洋の東西を問わず、なにかがあると年寄りの経験や知恵を頼りにしたものです。
今でも、おばあちゃんの知恵だとか、職人さんの伝統技といった形で辛うじて残っていますが、最近は年を取ればすぐに施設に放り込んでしまう世の中です。
経験が全てではありませんが、未経験者だけで初めから思考錯誤するより、経験者の知見を活用した方が早く結論(仮説)を導き出せます。
実戦を通して人材を育てることもできます。
とはいえ、なにかと目新しいものがもてはやされる風潮では、あまり共感を呼ばないかもしれませんね。
そもそも、実際の改善活動では問題解決アプローチなど一々意識しません。
しかし、うまくいくこともあれば、そうでないこともあります。なぜ、うまくいったのかを考える時、そこには、重要なヒントやサポートをくれた第三者が存在することが少なくないのです。
人が重要な経営資源であり、問題解決はマンパワーによって行われることを考えれば、このアプローチを活用する価値はかなり高いと思います。
