S-パラメータとスミス・チャート —基本は大事—

現在のマイクロ波通信および光通信機器においてさまざまな部品や伝送線路が用いられています。

近年のようにデータの伝送容量が大きくなると通信速度もより高速になっており、それら通信機器に使用する回路および部品も、より精度を求められ、信号の伝送損失や反射損失をより少なくするための部品や回路設計が求められます。高周波・マイクロ波のエンジニアにとってはお馴染みですが、それらを設計する際に用いられるパラメータとしてS-パラメータというパラメータを使用します。S-パラメータは、簡単に述べると、回路または通信回線に入っていく信号と出てくる信号および反射して戻ってくる信号の関係を表す数値データのことです。

当社では、マイクロ波・光通信の通信機器に使用するワイヤボンドタイプの単層コンデンサ（SLC : Single layer capacitor）および金でパターンニングを施したアルミナ基板の製造販売をしており、当社の顧客からは、通信機器および伝送線路において、より損失の少ない回路設計をするためのシミュレーションを実施する際のパラメータとして、このS-パラメータのデータを求められます。

さて、ここでは、最初に、反射信号について述べることにします。高周波・マイクロ波信号を扱う場合や、高速パルス回路で tr　<　2tdが成り立つ場合（ここで、trはパルスの立ち上がり時間、tdは伝送路の伝搬遅延時間を表します）、その伝送路を「分布定数回路」として扱わなければなりません。ここで分布定数回路とは、回路や伝送線路に具体的な抵抗、コンデンサおよびコイルといった回路部品で構成するのではなく、仮想の回路部品が無限に分布している状態の回路を分布定数回路と呼びます。その反対に、有限個の具体的な回路部品で構成される回路を集中定数回路と呼びます。その分布定数の伝送路において負荷インピーダンスをZLとしたとき、反射係数ρという考え方が必要になります。なぜ、この反射係数という考え方が必要になるかというと、扱う信号の周波数が高くなればなるほど、反射して戻ってきてしまう信号が増大していきます。高周波・マイクロ波回路の設計においては、いかに、反射して戻ってきてしまう信号をより少なくし、効率よく信号を伝達させるための設計を求められます。

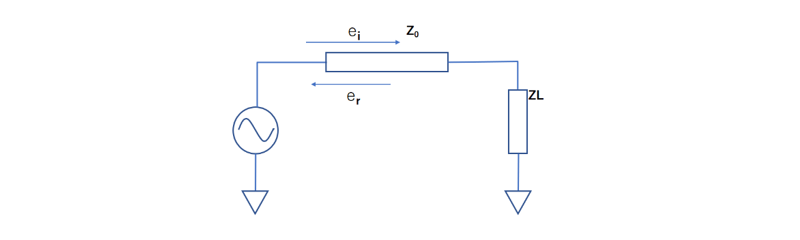
たとえば，特性インピーダンスZoの伝送線路の左記に負荷ZLを接続したとします（上図）。
このとき、反射係数ρを特性インピーダンスZoと、負荷インピーダンスZLで表すと次の式になります。

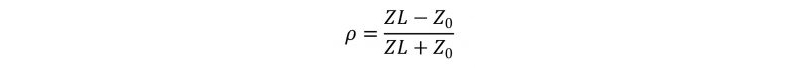
この時に、実際に反射係数ρを求めるためには、まず、入力した電圧をeiとし，反射してくる電圧をerとすると、次の計算式により求まります。

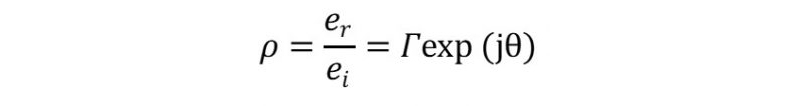
他に、伝送路における伝送信号と反射信号の関係を示す言葉として、電圧定在波比（Voltage Standing Wave Ratio=VSWR）というものがあり、高周波・マイクロ波の技術屋の間では、このVSWRという言葉も頻繁に使われます。この場合、反射係数ρとの関係は、次の式で示されます。

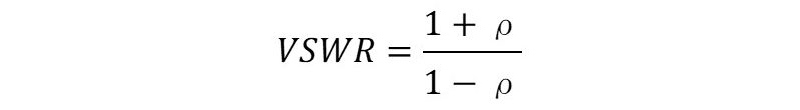
なお、ここで注意するのは，高周波・マイクロ波におけるeiとerはスカラー量ではなく、ベクトル量になるため、単純な直流電圧計や交流電圧計で測定することは不可能です。

そこで、ベクトル・ネットワーク・アナライザ（VNA）の登場です。

VNAの外観

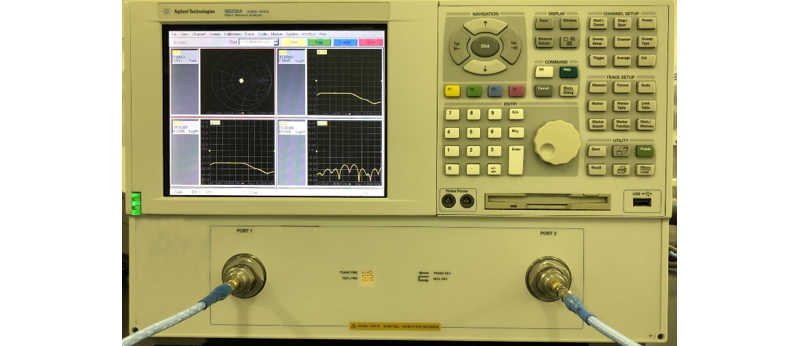
ベクトル・ネットワーク・アナライザは、被測定物に高周波信号を入力し、伝送損失や反射損失を測定する測定器です。たいへん高価な測定器ですが、内部にある方向性結合器により被測定物への入力信号の大きさ、被測定物に入力したものの反射して戻ってきた信号の大きさ、および、被測定物を通過して出力された伝送信号の大きさを検出します。反射係数は、その入力信号と反射信号を検出することにより、反射係数ρを求めます。これら測定した値を、Sパラメータと呼び、反射信号はS11、伝送信号はS21、被測定物の出口側から信号を入力した場合の反射信号はS22、伝送信号はS12といい、すべて数値で表されます。

ベクトル・ネットワーク・アナライザでは、信号を電圧や電流に分けて測定することは困難なため、これらの値の算出には、電力でおこなっています。

Sパラメータの数値データの例 （ある増幅用半導体デバイスのデータです）

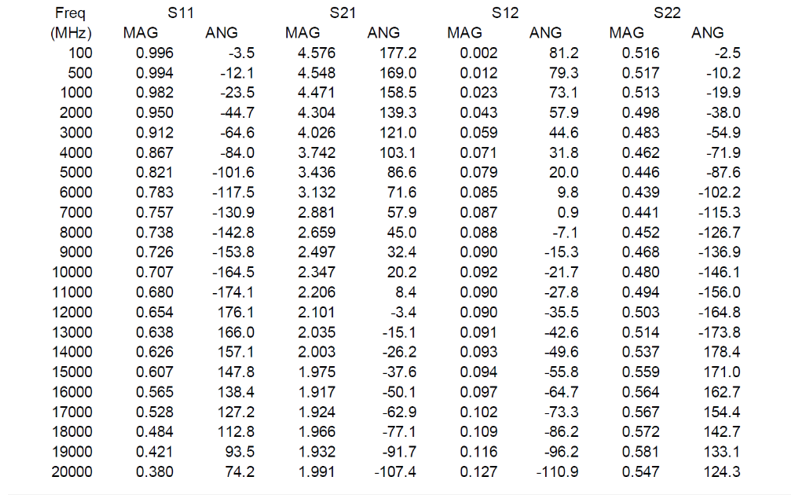
ところで、ベクトル・ネットワーク・アナライザで測定したデータでは、反射係数はΓで表現されていることが良くあります。このときのΓは次式で示されます。

ベクトル・ネットワーク・アナライザでの測定において、反射信号の測定データをリターンロス（Return Loss=R.L. : 反射損失）と呼びdB（デシベル）で表すことも一般的です。

ここで、VSWR、 反射係数Γ、反射電力（%）、反射損失（dB）、伝送電力（%）、伝送損失（dB）の関係は、次の表のようになります。

計算式は、

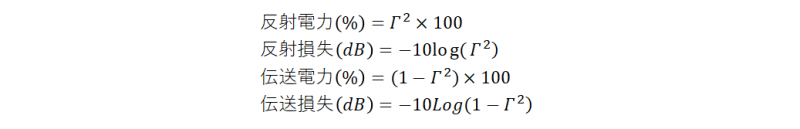
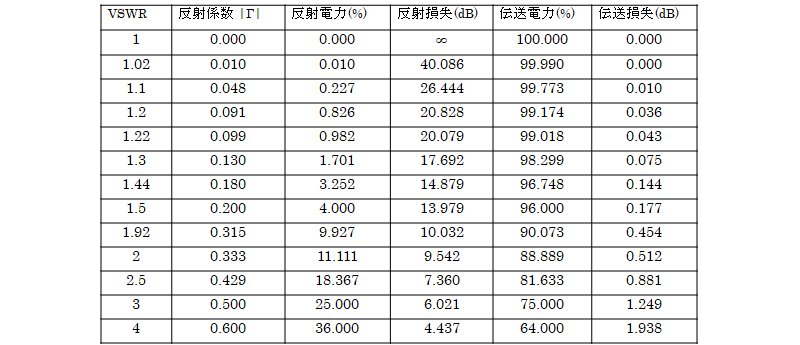
さて、設計をしていると、Γとθといった量ではなく、インピーダンスZ(Ω)=R+jXでの値を知りたいこともあります。

例えば、マイクロ波帯増幅器を設計する際において、マイクロ波帯の信号を増幅するデバイスGaAs-FETを使用することにして、GaAs-FETの入力信号ラインと出力信号ラインにおいてインピーダンスマッチングをするための回路設計をおこなう必要がありますが、その際に、インピーダンスにおける虚部であるjXのXの値を求める必要があります。しかし、デバイスのデータシートを見ると、Γ（Mag）とか θ（Ang）で表されているS-パラメータが記載されています。しかし、知りたいのはインピーダンスにおけるR（実部）とX（虚部）の値です。さて、ここでどうしたものか。

これは、反射係数Γ（またはρ）の定義にしたがって式を変形させれば，このΓとθをインピーダンスの形に変形できるのです。ここで、このΓ（Mag）とθ（Ang）からZ=R+jXの変換式を導いてみることにします。

オイラーの式より

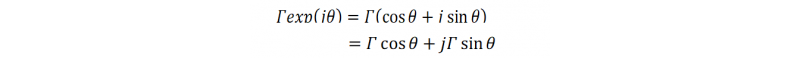
ここでZを規格化インピーダンス（実際のインピーダンスを特性インピーダンスZoで正規化したインピーダンスのこと）で考えると

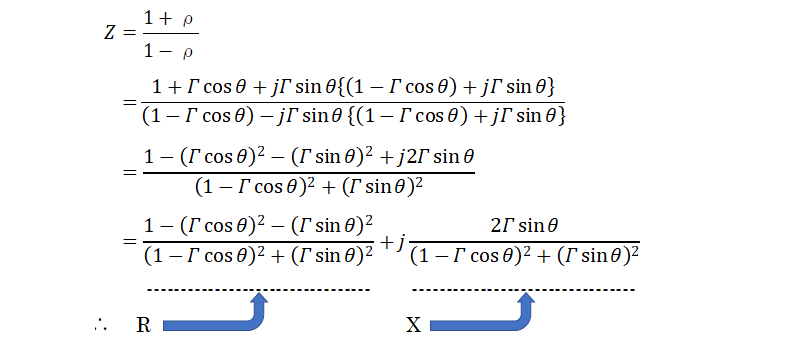
となります。

実際の値にするには、それぞれZo（50Ω）を掛けてやればいいことになります。

さて、ここで、近年は高周波・マイクロ波機器を設計するにも、シミュレータというソフトウエアが充実してきており、高周波・マイクロ波のエンジニアもこぞってシミュレータを使って設計をおこなうことが主流です。あまりにもシミュレータが高機能であるため、近年のエンジニアは設計をシミュレータ頼りにしてしまっており、基本を知らずして設計をおこなっているということが事実としてあげられます。

何しろ、シミュレータ上でパラメータを与えると自動的に計算し、最適な解を見つけてくれるので、こんな便利なものはありません。

そこで、そうやって設計をおこなっているエンジニアに、基本的な事を質問すると、答えられなかったり、わからないという答えが返ってきたり。

シミュレータで計算や設計した結果で物が完成すれば、それはそれでいいのかもしれません。しかし、基本がわからないとなると……考えものですね。

例えば、増幅器を設計するとします。

ある程度の基本設計をしたのちに、シミュレータでシミュレーションをおこない最適化をするというのが近年の設計法。

では、デバイスのデータシートに記載されているS-パラメータはどのように使うの？

デバイスのカタログには、次のようなデータが記載されています。これは、先ほどのS-パラメータの数値データの例のデバイスと同じデバイスのS11、S22のスミス・チャートとS21、S12の極座標グラフです。

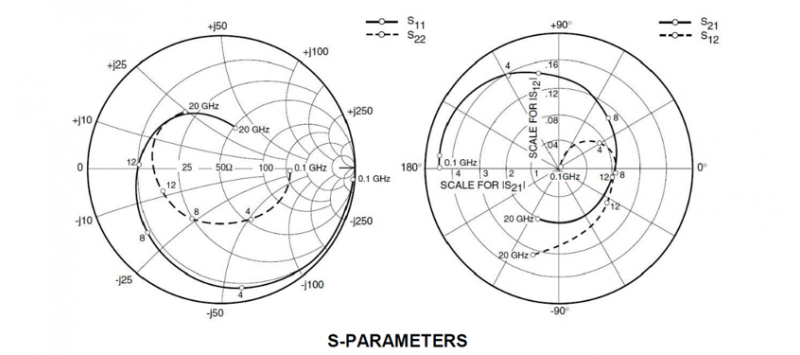
さてさて、例えば、このデータから8GHzで最大の利得を持つ増幅器を設計せよという課題があったら、シミュレータを使用する場合は、このS-パラメータをs2pファイルにして8GHzで最大の利得が得られるように設定をして最適化をかけ、マッチング回路を決定しますが、では、その基本としてシミュレータを使用しない場合は、どうやってマッチング回路を設計していくのか。

基本を理解しているうえでシミュレータを使って設計している人は簡単に出来ることでしょう。しかし、最初からシミュレータでの設計を教えられた人や勉強した人は、この数値データを与えられてもシミュレータを使わないと何もできないのではないでしょうか。

余談ですが、私は、ずいぶんと昔になりますが、次のように教えられました。そうして、そのようにやってきました。

「基本わからずして技術者とは言えない。手計算ができずしてシミュレータだけで安易に設計をしてしまうのは本当の技術者とは言えない。まず、基本を理解したうえで手計算をして、次にシミュレータで検証をしながら設計精度をあげろ。最初からシミュレータだけで設計すると、与えたパラメータによりシミュレータによる最適化の結果、とんでもない値に最適化され、結果的に出口は同じでも、途中がとんでもない回路が出来上がる。基本に忠実にシンプルに回路設計し、シミュレータで検証と最適化をおこなうのが正しい設計のやり方。それが出来ない技術者は、単にうわべだけの技術者である。」と。

また、仕事において、同様にしばしば直面することですが、完成したものの測定をおこなった時、測定器に表示されている値は正しい値ですか？ 予め、計算した値または設計した値と比べてどうなのですか？ 測定の方法と測定系は正しいですか？ 測定系の校正は正しくおこなわれていますか？ こちらも同じで、測定器で測定して得られた値を、検証もせずに正しいと思い込んで、良し悪しを判断してしまう人がいます。まずは、基本になるべきことは、その値が、正しいのか、もしくは正しくないのかの検証と、基準になる値はあらかじめ計算して求めておくことが重要です。

そういうわけで、今までのサマリーです。

では、先ほどのS-パラメータの数値データとスミス・チャートを使用して、8GHzで最大利得が得られる増幅器の設計をしてみましょう。ここではスミス・チャートを使ってマッチングをとっていく方法を説明するので、通常は8GHzという高い周波数帯では、分布定数を使用しての設計をおこなうのですが、ここでは簡易的に集中定数を使っての設計例をおこなっていきます。

ここで、先のS-パラメータの表にある増幅デバイスの8GHzのS-パラメータにおいて、 S11のMagは、0.738 で、Phaseは、-142.8°。また、S22のMagは、0.452で、Phaseは、-126.7°です。

S11とS22は、それぞれデバイスの入力側と出力側に信号を入力した時に、反射して戻ってきてしまう信号を数値化して表しています。このデバイスの入力側と出力側のインピーダンスを、一般的な高周波での特性インピーダンスである Z0=50Ω へ、マッチングをとる回路を設計していくことにします。

マッチングをおこなうことにより、デバイスに入力する高周波信号とデバイスから出力される高周波信号において、反射が抑えられ、回路に入力された高周波信号は最大限にデバイスに入力されますし、デバイスで増幅された高周波信号は、最大限に出力されることになります。

ここで、高周波・マイクロ波のエンジニアにとって必須アイテムのスミス・チャート（Smith Chart）というグラフの登場です。このグラフは、インピーダンス・チャートとも言います。

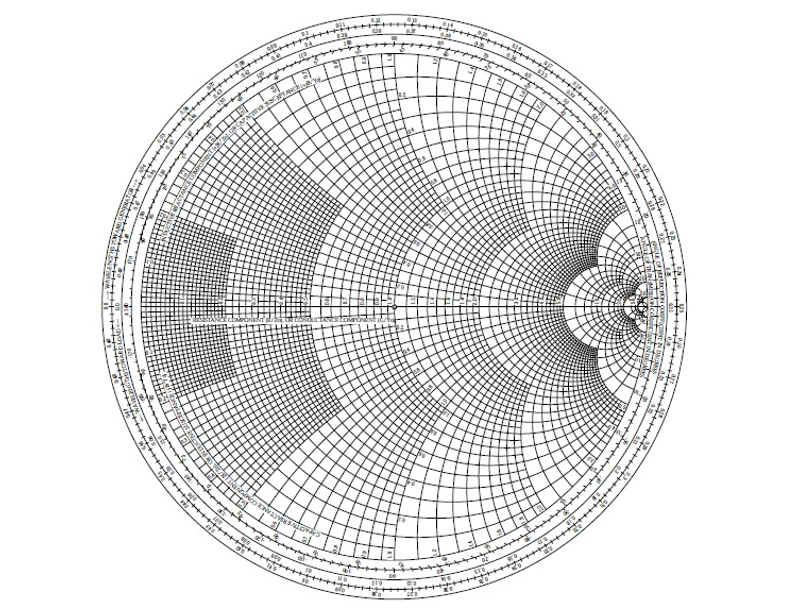
このスミス・チャートは、反射係数と位相角およびZ = R +jXのR（実部）とX（虚部）をあらわすものですが、そのままS11のMagは、0.738 で、Phaseは、-142.8°。また、S22のMagは、0.452で、Phaseは、-126.7°をプロットしてもいいし、50Ωで正規化したRとXの値でプロットしてもいいのですが、ここでは、先に導いた式を使用して、S11をインピーダンス変換した、RとXの値をプロットしていくことにします。

そうすると、S11のインピーダンスZ = 8.37 + j (-16.4)になります。

S22のインピーダンスは、Z = 22.8 + j (-20.8)になります。

まず、S11のZ = 8.37 + j (-16.4)を、スミス・チャート上にプロットすると、次の図のようになり、先のカタログのスミス・チャート上のS11の8GHzのプロットと同じ位置にプロットされることがわかります。ここでは、次の作業のために、イミッタンス・チャート（スミス・チャートとその逆数を表すアドミッタンス・チャートを合成したチャート）を用い、それにプロットしてみました。次のグラフ上、DP1と表記しているのが、このデバイスの信号入力端子部のインピーダンス（8GHzの信号の反射）を表しています。これを特性インピーダンスの50Ωと整合をとるために、ここでは、集中定数として、キャパシタンスとインダクタンスを使用して整合をとっていきます。ここで先のスミス・チャートの図で、円の中心は1ですが、特性インピーダンスが50Ωの場合は、正規化して中心が50Ωになります。

（以下、解像度が悪いため画像がたいへん見えにくくて申し訳ありません）

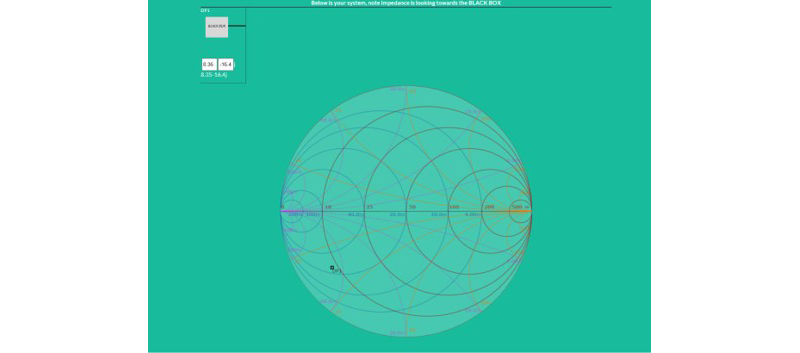
50Ωに整合をとるために、このデバイスの入力部（DP1のBlack Box : 図の左上参照）に向けてキャパシタンスとインダクタンスを付け、それぞれの定数を決めていくと（下図）、インピーダンスの軌跡が動き、最終的にこのデバイスの入力部が50Ωに整合がとれました。

定数の計算方法ですが、まず、起点がZ (Ω) = 8.37 + j (-16.4)ですので、スミス・チャート上の、その点にまずプロットします（若干、図の中の表示がズレていますが、ご容赦ください）。次に、中心の50Ωに整合をとるために、スミス・チャートまたはアドミッタンス・チャートにおいていくつかの経路を想定してみます。最短でかつ、実現できそうな経路を想定して整合回路を決めていきます。そこで、次の図にある経路で回路定数を決めていくことにします。DP1 = Z (Ω) = 8.37 + j (-16.4)から、スミス・チャートの抵抗円上において、次の点DP2を決めます。DP2のインピーダンスは、DP2 = Z (Ω) =8.37 + j(-36.3)です。回路素子としては、直列にキャパシタを用います。次に、アドミッタンス・チャートのコンダクタンス円上において、次の点DP3を決めます。DP3 = Z (Ω) = 50 + j(-75.5)です。回路素子は、並列にインダクタを用います。最後は、50Ωに整合をとるため、次の点は中央の Z = 50 + j (0)になります。回路素子は、直列にインダクタを用います。

さて、ここで、最初のキャパシタの容量値を求めることにします。

まず、DP0から、DP1までのインピーダンスの虚部の差は、-36.3-(-16.4) = -19.9 Ωですので、8GHzにおける容量の計算式

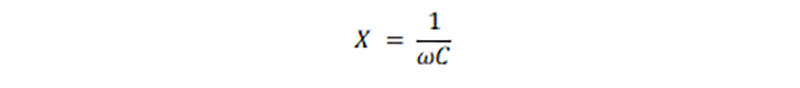
より

になります。

次に、DP1からDP2に至る経路は、素子を並列に接続するためアドミッタンス・チャート上のコンダクタンス円を見て計算します。アドミッタンスは、Y = G + jBであらわされます。アドミッタンス・チャート上において、DP1のアドミッタンスは、

Y (S) = 6.2246m + J (26.06m)。DP2のアドミッタンスは、Y (S) = 6.097m + j (9.207m)。

これらの虚部Bの差は、26.06 – 9.207 = 16.853m。

これにより、

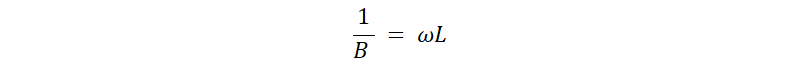
より

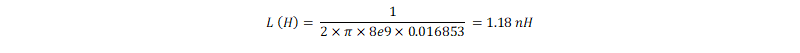
になります。

ここでの計算は、並列接続であることにより、インピーダンスではなく、アドミッタンスで計算することにより、この値を得ることができます。

最後は、直列のインダクタの計算ですが、こちらは、スミス・チャートにおいて、

Z = 50 + j (0) と DP3 = Z (Ω) = 50 + j (-75.5)の虚部の差、75.5 Ωのインダクタンス値を求めればいいので、X = ωL より

になります。

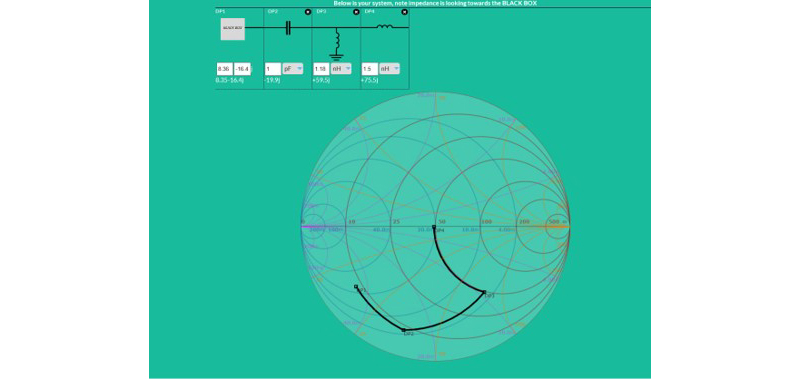
これで、入力側の整合回路の設計は完了です。（このプログラムでの画面では、この場合、Black Boxで表したデバイスの右側に接続したキャパシタなどの素子の右端が信号の入力部になります）

Note :

ここで、やってはいけないこと。

例えば、上記のインピーダンス=8.36 + j(-16.4)において、50Ωに整合を取る場合、チャート上、実部まで軌跡を移動し、jX=0にした後、41.64Ωの抵抗を直列に入れると、8.36 + 41.64 = 50となり整合はとれるが、高周波信号が抵抗を通過することになり、信号が減衰してしまうため整合をとる意味がない。従って、整合をとる場合は必ずキャパシタンスまたはインダクタンスを使用し、理論上は損失が発生しない虚部を動かすことによって整合回路を構成しなければなりません。

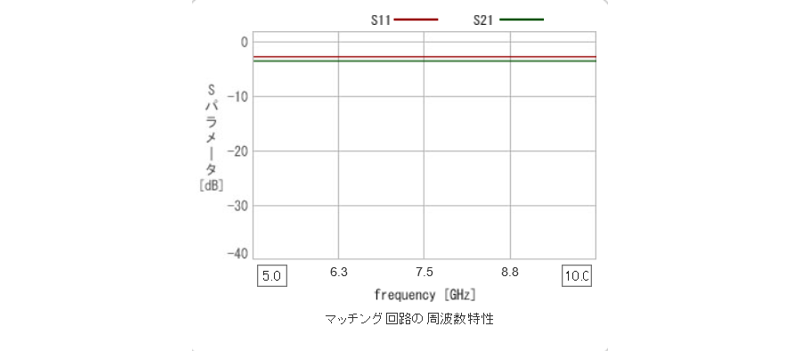
もともと、整合回路がない状態において、素子へ入力した信号の反射特性、および、出力側の反射特性は、下図（左 : グラフタイトルがマッチング回路の周波数特性になっていますが、正しくは、マッチング回路なしの場合の周波数特性に読み替えてください）であり、反射・損失とも大きいですが、計算によって得られた整合回路を取り付けることにより、下図(右)のようになり、8GHzにおいて損失は最小となり、反射も極めて小さくなります。

同じように、デバイスの出力側を50Ωへの整合をおこなっていきます。S22の Z = 22.8 + j(-20.8)を、スミス・チャート上にプロットすると、

やはりここでもDP1と表示しています。

同じように、50Ωに整合をとるために、キャパシタンスやインダクタンスを使用していくと、次のようになります。

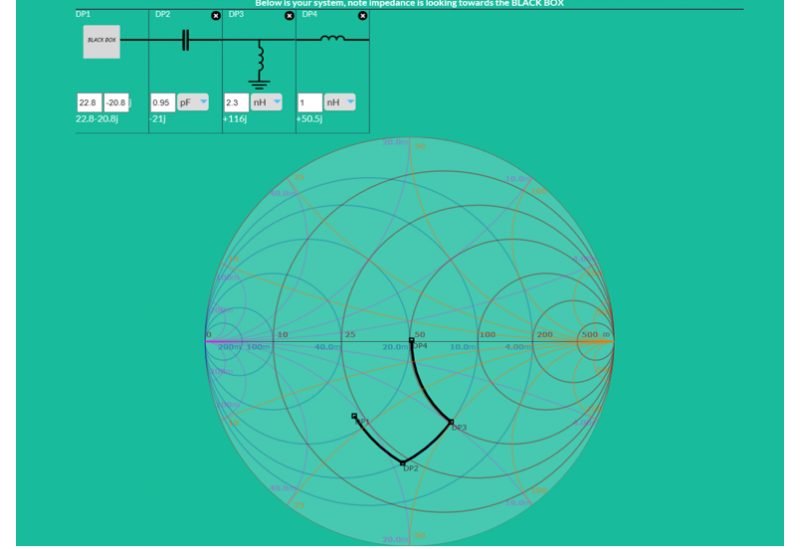
ここでは、周波数特性のグラフは割愛させていただきます。

これで、デバイスの入力側に続いて、出力側の整合回路の設計が終わりです。これで回路を製作すれば、理論上は8GHzにおいて、このデバイスの最大利得が得られる増幅器を作ることができます。また、8GHzという高い周波数を使う回路であるため、集中定数回路で整合回路を構築しようとすると特にインダクタンスが非現実的な値になってしまっています。先に述べたように、ここでは考え方や方法の説明のために集中定数での説明を行いましたが、本来は分布定数回路で設計をしなければならないため、別の機会では分布定数での整合回路の設計法を述べていきたいと思います。

さらに、高周波・マイクロ波回路の設計においては、様々な要素が絡み合うため、実際には、そうそう単純なものではないということを付け加えておきます。

なお、このデバイスの入力部と出力部を50Ωに整合をとる方法は、イミッタンス・チャートを眺めると、いくつものパターンがあることがわかります。上記は、その中の一つにすぎません。

基本を知っていれば、一番楽に整合をとる方法がすぐに見えます。シミュレータでは、最初のパラメータの設定によっては、一番楽に整合をとるパターンではない解に導かれることも多いので、まず、上述の説明により、いきなりシミュレータを使って設計を始めるのではなく、基本に従って、ある程度の解を求めておいてからシミュレータを使用するという方法をとると、最適な解を求める近道になります。

Tweet