2019/8/28 テクダイヤ技術向上ブログ
教科書では学べない、これが本当のコンデンサのインピーダンス計算法
当社は、創業以来、セラミックで出来た誘電体に金属膜(電極)を付けた、無線通信機器および光通信機器に多く使用されるワイヤボンディングタイプのコンデンサの開発、製造販売をおこなっています。次世代通信技術である5Gにおいても、IoTの発展においても、それらに使用される電子機器にはコンデンサは不可欠な部品であるため、今後も多くの需要が見込まれています。
当社が製造販売をおこなっているコンデンサは、誘電体を電極(金属膜)で挟んだ形状のため、世の中に数多く販売されている積層タイプのコンデンサとは異なり、名称も単層コンデンサ、単板コンデンサまたは単純にチップコンデンサと呼び名は様々で、英語での名称シングル・レイヤー・キャパシタ(Single Layer Capacitor)の頭文字をとって、SLCとも呼びます。ここでは、以後単純にコンデンサと記述します。
コンデンサのインピーダンスの計算
さて、このコンデンサですが、通信機器に使用する際、重要となる特性があります。当社では、設計開発の段階および製造時での製造バラツキによるその特性の評価として、通信機器において十分な性能が発揮できるように保つため、製造業としては当然のことですが、試作段階から様々な特性評価をおこない十分な性能を保っていることを監視しております。
もっとも重要な項目は、容量素子であるコンデンサですから、その「容量値」の評価。当社のコンデンサは、ワイヤボンドタイプとしてよく使用される1pF以下から10,000pFを超える容量値の製品を幅広くラインナップして販売しております。
次に重要なのが、「損失」。損失が大きいと通信機器の市場向けである当社のコンデンサの特性としてはよくないので、損失は性能として重要なファクターになっています。この損失は、コンデンサのインピーダンス特性を評価することにより求まるのですが、容量値と共に損失のデータをインピーダンス特性から容量値や損失に換算し表示するLCRメーターという測定器により評価をおこなっています。
ここで、コンデンサのインピーダンスとは、教科書や参考書には、次の計算式で表されています。
Z = 1/ωC (Ω) ・・・(1)
インピーダンスZは、直流における抵抗(Ω)と同じ意味を持つ、交流における抵抗でインピーダンスといいます。単位は、直流抵抗の単位と同じΩです。
ωは、2πf。いわゆる角周波数と呼ばれるものであり。fは、周波数(Hz)が入ります。1MHzの場合は、1×106(Hz)です。
Cは、コンデンサの容量値(単位はF)。仮に容量値が100pFの場合は、100×10-12(F)として、これらを(1)の計算式に当てはめ計算をおこなうと、コンデンサのインピーダンスは、約1,592Ωになり、周波数が10MHzの場合は、約159.2Ωというように周波数が高くなればなるほど、コンデンサのインピーダンスは、無限に小さくなっていきます。
しかし、コンデンサは、容量の成分(C)だけではなく、損失の元になる抵抗成分(R)や、さらにインダクタンス成分(L)も含まれています。インダクタンス(L)は、コイルと同じ機能を有しています。
そこで、世の教科書や参考書を初めweb上のコンテンツにも、コンデンサの等価回路は次のように書かれて説明されています。
ここで、インダクタンス(L)のインピーダンス(Z)の計算式は、Z = ωL (Ω)であるので、
この等価回路上では、コンデンサのインピーダンスを求める計算式は、
Z(Ω) = R + jωL + 1/jωC = R + j(ωL ‐ 1/ωC) ・・・(2)
という、抵抗Rが実部を、j(ωL ‐ 1/ωC)は虚部で表わす複素数を用いた式になります。
コンデンサにおいて、実部のRを等価直列抵抗(Equivalent Series Resistance = ESR)と呼びます。
虚部のj(ωL ‐ 1/ωC)は、jXとも表し、リアクタンスとも呼びます。
ここで、前述の「損失」は、tanδまたはDF(Dissipation Factor)で表わし、
tanδ(DF) = R/X ・・・(3)
の式により求まります。
また、(2)の式において絶対値を求める計算式は、
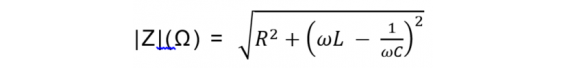・・・(4)
コンデンサのインピーダンス(Z)は、(4)の式により ωL = 1/ωCの時に最小になり、Rの値のみになることがわかります。世の教科書などには、通常はここまでの解説がされています。
さて、本当にこれで正しいのか。
ここで、当社で製造販売しているコンデンサ(容量値は390pF)を、インピーダンスアナライザで測定してみましょう。
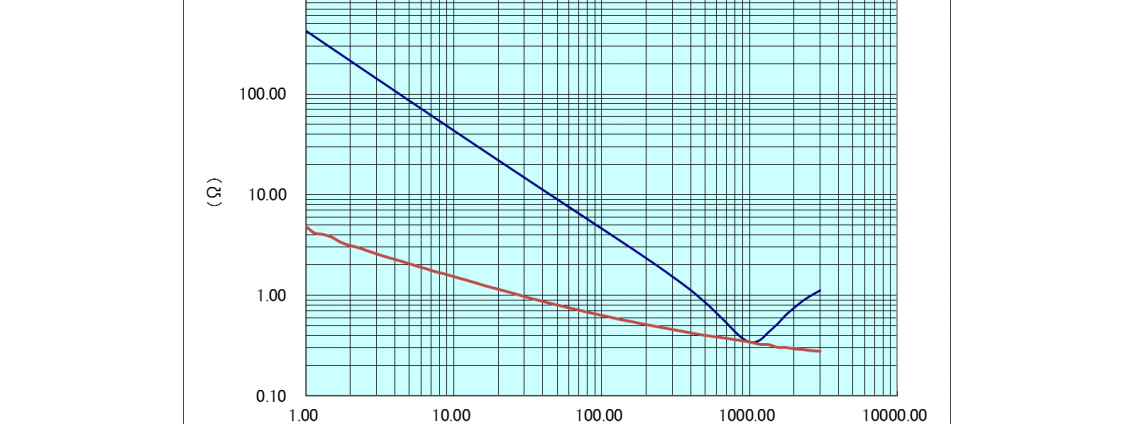
次のグラフは、コンデンサのインピーダンスZと、Rを測定し、その結果を表わしたグラフです。ここで、横軸が周波数。縦軸はインピーダンスZと、等価直列抵抗(ESR = R)の値になります。
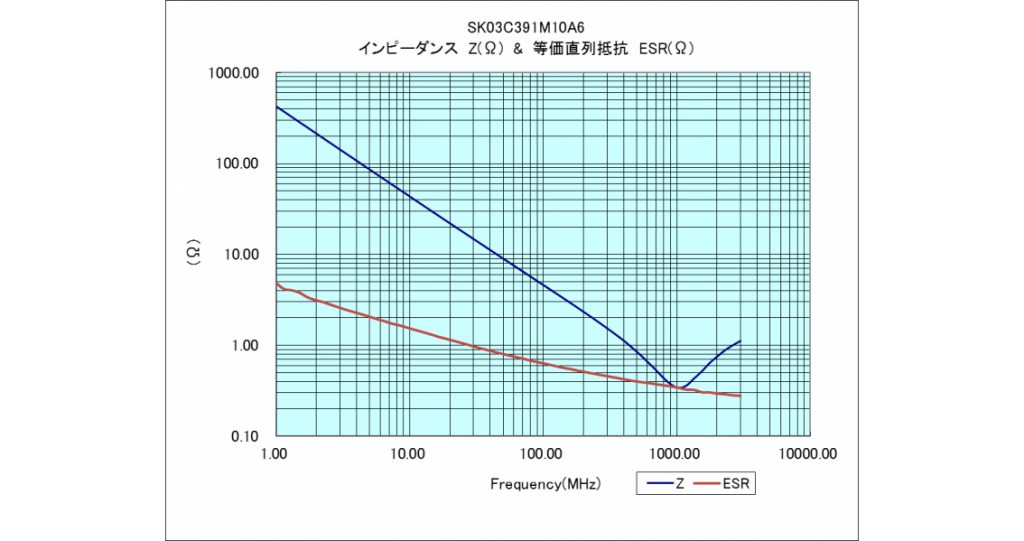
インピーダンスZの値は、虚部にあるω(=2πf)の変数である周波数f(横軸)の値が変ると変化し、このグラフでは、周波数の低い領域から1000MHz付近までは、容量成分(C)の周波数特性によりインピーダンスは低くなっていきますが、1000MHz付近を境に、今度は周波数がさらに高い領域では、インダクタンス(L)の値が支配的になり、インピーダンスが高くなっていることが読み取れます。
次に、等価直列抵抗(ESR)ですが、うん・・・? 上述のコンデンサの等価回路における計算式(2)でのRの値には、変数(2πfのfである周波数)が使われていないのに測定で得られたRの値が変動している・・・・???
インピーダンスを求める式(2)では、周波数が変ってもRの値は変わらないはずだが・・・??
身の回りのエンジニアにこの事を質問してみると、
「・・・・???」
他のエンジニアに質問してみても、
「はいっ、・・・・・???」
ここで、某放送局の番組で人気のチコちゃん風に、
「ボ－ッと仕事してんじゃねーよ!」
と言われても・・・。
なぜRの値が変化してしまうのか ～ こんなこと教科書に書いてないよ
そうなんですよね。教科書や参考書にはこんなことは書いていないし、webを探しても、その理由が書かれたコンテンツはなかなか見つかりません。
では、そのRの値が変化してしまう理由を解説しましょう。
コンデンサの等価回路を、さらに詳しく書くと次のようになります。
ここで、Rpは、コンデンサの絶縁抵抗分とみなしてください。
この等価回路により、コンデンサのインピーダンスZは
Z(Ω) = Rs+(Rp/(1+ω2Rp2C2) + j((ωL-ω2Rp2C+ω3Rp2LC2)/(1+ω2Rp2C2))
という計算式で表わされ、左側の下線部が実部 = R(ESR)の値になります。
つまり、実部のRの箇所にも、変数であるω(=2πf)が入っているため、教科書や参考書に書かれている事とは異なり、Rの値が動いてしまうのです。
これで疑問は解消されましたね。
最後に
仕事上、いろいろな物を設計開発し、その試作品や製品の測定をしてきましたが、教科書や参考書に書かれている事と異なるデータが得られる事がよくあります。
これは、教科書や参考書は、ごく一般的な基礎的事項が書かれているだけのみであるので、仕事中に、「あれっ? 書かれている事と違う」という疑問が生じたら、その理由を考えてみることが重要です。
また、試作品や製品のデータを取得する際は、漫然と測定して得られたデータをそのまま鵜呑みしてしまうと大きなケガを負ってしまいます。得られたデータが正しいかどうかの判断基準としては、やはり理論計算の結果と比較して、近い値なのか、理論値とかけ離れた値なのかを、その判断基準を持って測定すること。さらに、正しく測定しているという前提で、上述のように、計算式は合っているのに、計算とは異なるデータが得られるような場合は、教科書や参考書では得られない何かが潜んでいるはずです。そこを探究するのがエンジニアとしての醍醐味です。
《おススメ人気記事》
シート抵抗とは
テクダイヤの超高誘電率セラミックコンデンサ、「ALTAS®」とは
■テクダイヤ技術向上ブログ
テクダイヤの開発・生産に携わる、若手エンジニアによる公式ブログ。技術情報はもちろん、失敗談や体験談など有益な情報を幅広くお伝します。
