意外と役に立つ？大雑把なサンプリング数の設定方法

検出に必要なサンプル数はいくつ？

一定の割合で含まれているものを検出するために、何個くらいサンプリングすればいいか考えさせられる場面はままあるかと思います。

ものづくりの現場では、
「ロットが1%以上の不良品を含んでいるかどうか確認する為にどのくらいサンプリングしたらよいか？」であったり、
日常生活においては、
「0.5%で当たりが入っているクジであたりを引くためにはどの位クジを引かなくてはいけないか」
であったりします。

そのような場面で面倒くさい計算なしでラフにサンプル数を設定する方法があります。

それは「期待値が3になるくらいサンプリングする」ことです。

この方法では95%以上の確率で「不良品」や「アタリ」を引くことができます。
例えば「不良品」や「アタリ」の含有率が1%の場合、サンプリング数は300となります。

解説と実例

以下にどうしてこうなるのか解説します。
「不良品」は製造業として聞こえも悪いし、縁起も悪いので、以下では「アタリ」とサンプリング数で示します。
アタリの含有率1%のクジを1回引いて外れる率は 99%です。
アタリの含有率1%のクジを2回引いて2回とも外れる率は 99%×99% = 98.01%です。
アタリの含有率1%のクジを3回引いて3回とも外れる率は 99%×99%×99% = 97.0299%です。

これを一般的な式で表すと、

1回もアタリを引かない確率：P
アタリの含有率：α
サンプリング数(クジを引いた回数)：n

として、

P = (1－α)^n

となります。

アタリを少なくとも1回以上引く確率は1－Pなので、

少なくとも1回はアタリを引く率 = 1－(1－α)^n

となります。

サンプリング数が「期待値が3になる回数(アタリの含有率1%なので300)」の場合、

少なくとも1回はアタリを引く確率 = 1－(1－0.01)^300 = 95.1%

となります。

この計算結果を様々な「アタリ」の含有率α、サンプル数nについて表にすると以下のようになります。
少なくとも1回はアタリを引く確率は全て95%以上となっています。

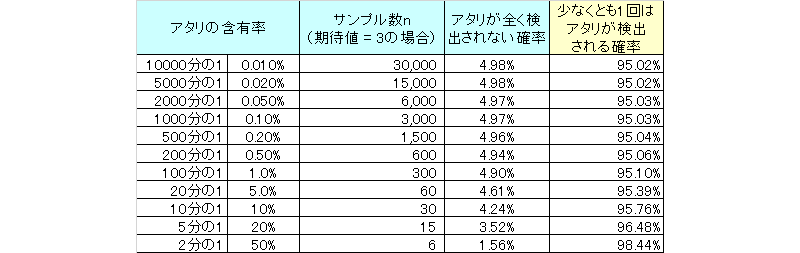
複雑な計算なしに暗算でサッとサンプリング数を設定できますので、ご活用いただけるかと思います。

期待値が2、1、0.5の場合はどうなるの？

因みに、期待値2、期待値1、期待値0.5の場合は以下のようになります。

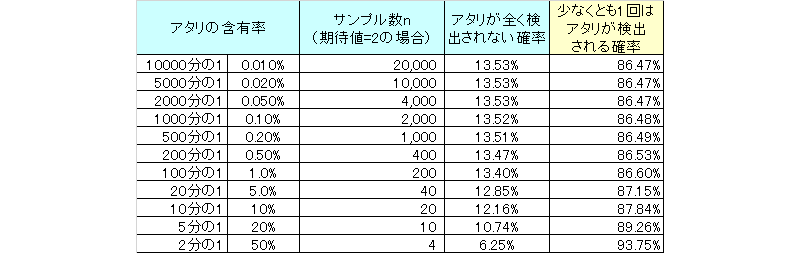
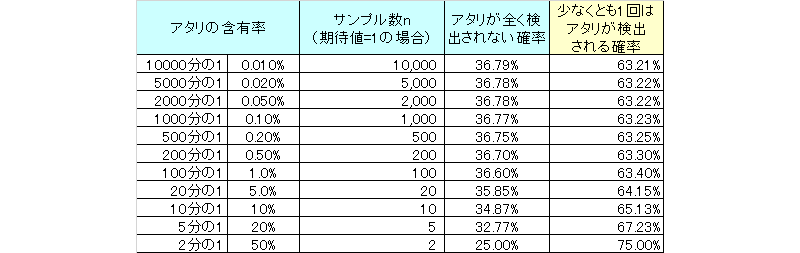
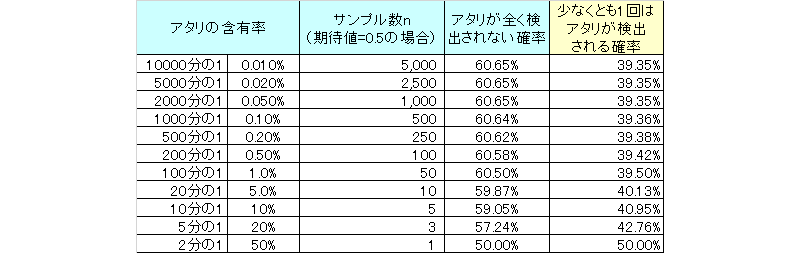
期待値1と聞くと普通にアタリを引けそうですが、計算上は6割程度しかアタリを引くことはできません。

ほぼ確実(95%)までもっていくには3倍の努力が必要。

一方、半分の努力(期待値0.5)でも4割は上手く行く。

人生の難しさを表しているように見えてなりません。

Tweet